SICP 1.2 - Procedures and the Processes They Generate, Part 1

Read the chapter here

In writing this, I wound up going on a bit of a sidequest in figuring out how to get my Ulysses and Ghost integration to work how I wanted them to. You may enjoy reading about that.

Notes

1.2.1 - Linear Recursion and Iteration

This section talks about ways of computing factorials. It gives this as the factorial function:

$n! = n ⋅ (n - 1) ⋅ (n - 2) ⋯ 3 ⋅ 2 ⋅ 1 $

It then gives this as a way of computing factorials:

$ n! = n ⋅ [(n - 1) ⋅ (n - 2) ⋯ 3 ⋅ 2 ⋅ 1] = n ⋅ (n - 1)!$

It translates this method of computing into a function:

(define (factorial n)
  (if (= n 1) 
      1 
      (* n (factorial (- n 1)))))

I find this straightforward so I won't belabor it.

It then introduces an alternative, iterative approach to computing a factorial, that involves keeping a running product and using a counter. Basically, you multiply the running product by the counter, and then increment the counter, until the counter exceeds the value of the factorial you're seeking, at which point you return the product.

(define (factorial n) 
  (fact-iter 1 1 n))

(define (fact-iter product counter max-count)
  (if (> counter max-count)
      product
      (fact-iter (* counter product)
                 (+ counter 1)
                 max-count)))

Here are these two factorial computation methods in graphical form:

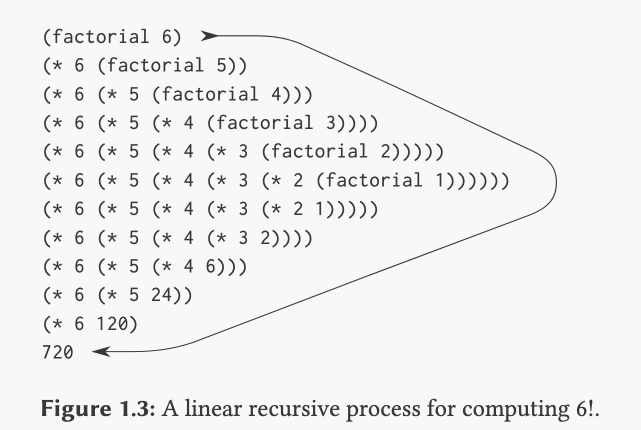
The recursive process depicted in Figure 1.3 builds up a chain of deferred operations that the interpreter has to keep track of. There's no chain of deferred operations in the iterative Figure 1.4 version. We just need to keep track of the product, counter, and max-count values. The book says that with the iterative version, you could theoretically stop the computation and restart it just with those values - they provide a description of the state of the process at any given point. They're all the info you need. But with the recursive process, there's some hidden info behind the scenes that is not encapsulated by the program's variables.

SICP then makes a point which I initially found confusing but understood after some thought:

In contrasting iteration and recursion, we must be careful not to confuse the notion of a recursive process with the notion of a recursive procedure. When we describe a procedure as recursive, we are referring to the syntactic fact that the procedure definition refers (either directly or indirectly) to the procedure itself. But when we describe a process as following a pattern that is, say, linearly recursive, we are speaking about how the process evolves, not about the syntax of how a procedure is written. It may seem disturbing that we refer to a recursive procedure such as fact-iter as generating an iterative process. However, the process really is iterative: Its state is captured completely by its three state variables, and an interpreter need keep track of only three variables in order to execute the process.

So basically, fact-iter calls itself, so it's recursive as a matter of what the literal code says. However, it doesn't build up that chain of deferred operations that "percolates" back up when arriving at the base case. It's recursive in literal fact but not recursive in its shape, in how it fundamentally works. The point is a bit abstract but I think I get it.

1.2.2 - Tree Recursion

SICP introduces tree recursion, using the standard Fibbonaci example.

(define (fib n)
  (cond ((= n 0) 0)
        ((= n 1) 1)
        (else (+ (fib (- n 1))
                 (fib (- n 2))))))

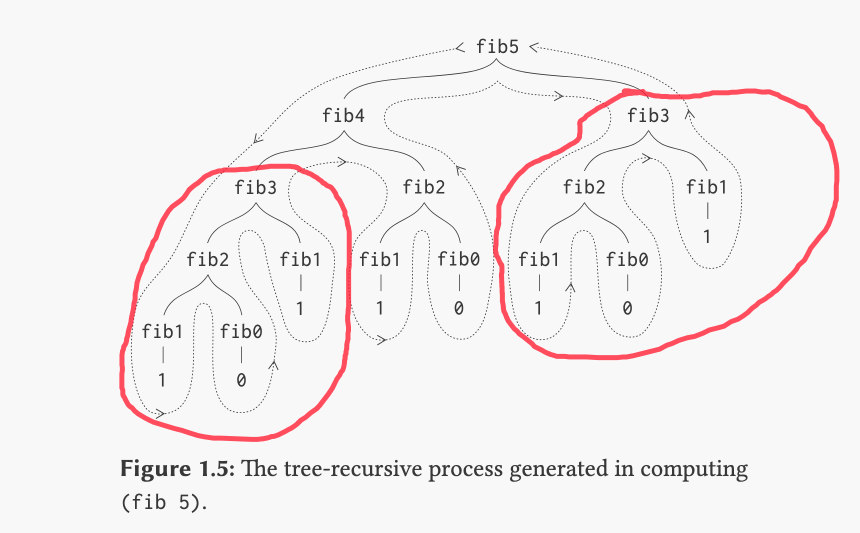
The book discusses how the number of times the procedure has to compute (fib 1) or (fib 0) is Fib(n + 1). It tries to contextualize how bad this is by talking about the golden ratio, but that part wasn't super clear to me. I may return to it later if it becomes relevant.

The book talks about how the number of steps required by the fibbonaci procedure increases exponentially but the space required (in terms of memory, I think) increases only linearly. I think you can see this on their tree. As we go from (fib 1) to (fib 2) to (fib 3) and so on, you can see that there are way more steps nested under the parent procedure compared to the next value down, which indicates exponential growth of the number of steps involved. But the parent procedure is only one level "higher" than the child, which indicates linear growth of the spaced required. I think the point here is that this implementation of the fibbonaci procedure is okay memory-wise but bad in terms of efficient CPU use.

They next talk about an iterative implementation of fibbonaci:

We can also formulate an iterative process for computing the Fibonacci numbers. The idea is to use a pair of integers a and b, initialized to Fib(1) = 1 and Fib(0) = 0, and to repeatedly apply the simultaneous transformations

$a \leftarrow a + b$

$b \leftarrow a.$

(define (fib n) 
  (fib-iter 1 0 n))

(define (fib-iter a b count)
  (if (= count 0)
      b
      (fib-iter (+ a b) a (- count 1))))

SICP makes the point that the recursive version of a process can be useful for understanding and designing a program even if an iterative process turns out to be better for other purposes.

Example: Counting change

The book asks us how many different ways we can make change of ﹩ 1.00, given half-dollars, quarters, dimes, nickels, and pennies, and wants us to write a procedure to figure that out. It suggests the following way to think about it:

Suppose we think of the types of coins available as arranged in some order. Then the following relation holds:

The number of ways to change amount a using n kinds of coins equals

• the number of ways to change amount a using all but the first kind of coin, plus
• the number of ways to change amount a - d using all n kinds of coins, where d is the denomination of the first kind of coin.

So to come up with a very simple and easy case, suppose we only had to worry about half dollars and quarters. According to what they are saying, the number of ways to make change for ﹩1.00 using those 2 kinds of coins would be the sum of the number of ways to change ﹩1.00 using all but the half-dollars (there is just 1 way in my example, with 4 quarters), plus the number of ways to make change on the amount ﹩1.00 - 50 cents (there are two ways - 1 half dollar and 2 quarters).

The reason this is true is basically this: either a sequence of coins for making change has a particular denomination of coin, or it doesn't. If it does have the denomination, then to figure out how many sequences use that denomination, we want to have a coin of that denomination in a "slot" of our sequence and then see what other iterations there are. Subtracting d from a represents putting a coin of denomination d in a "lot" in the coin sequence. Then we add the number of sequences that don't have a coin with that denomination. So with my simple example with half dollars and quarters we get:

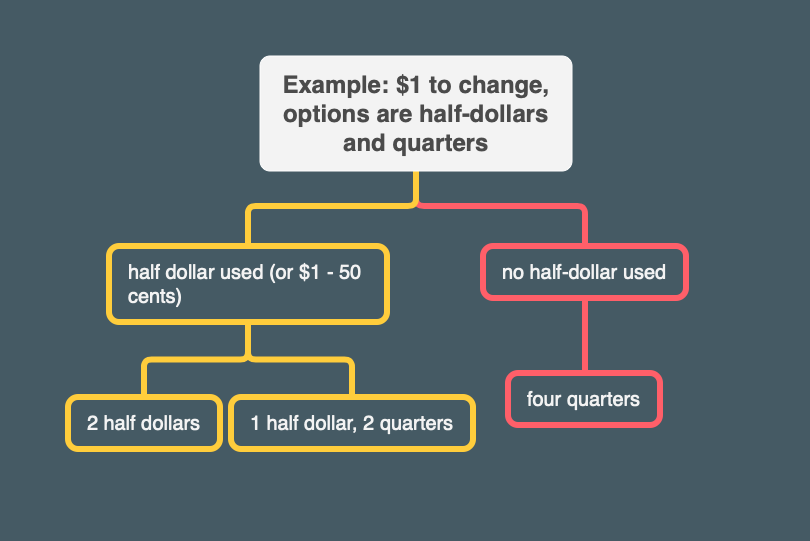
Note that I wrote out the entire coin sequence in the leaf nodes for the sake of clarity/readability.

Here's a tree where I added dimes:

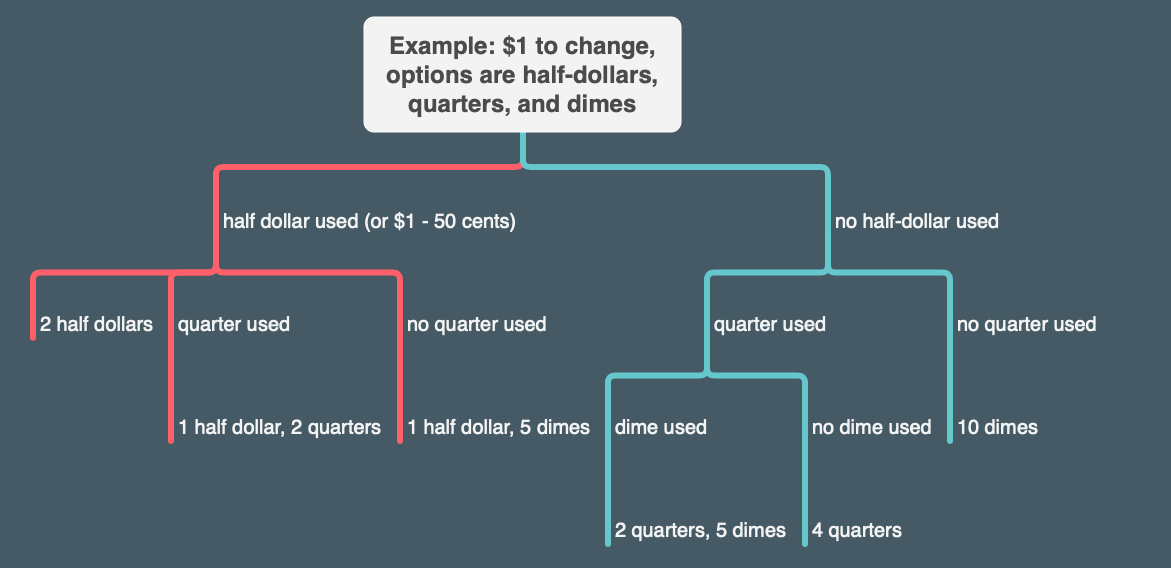
And here's an example the book suggests of considering making change on 10 cents with nickels and pennies:

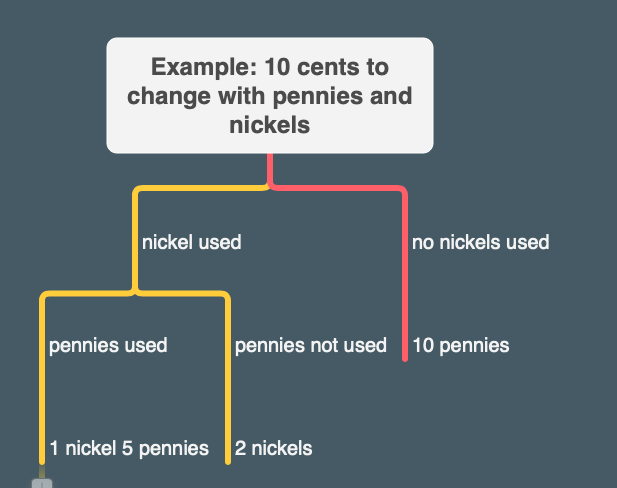
To see why this is true, observe that the ways to make change can be divided into two groups: those that do not use any of the first kind of coin, and those that do. Therefore, the total number of ways to make change for some amount is equal to the number of ways to make change for the amount without using any of the first kind of coin, plus the number of ways to make change assuming that we do use the first kind of coin. But the latter number is equal to the number of ways to make change for the amount that remains after using a coin of the first kind.

The book then proposes this rule and the following procedure:

• If a is exactly 0, we should count that as 1 way to make change.
• If a is less than 0, we should count that as 0 ways to make change.
• If n is 0, we should count that as 0 ways to make change.

(define (count-change amount)
  (cc amount 5))
(define (cc amount kinds-of-coins)
  (cond ((= amount 0) 1)
        ((or (< amount 0) (= kinds-of-coins 0)) 0)
        (else (+ (cc amount
                     (- kinds-of-coins 1))
                 (cc (- amount
                        (first-denomination kinds-of-coins))
                     kinds-of-coins)))))
(define (first-denomination kinds-of-coins)
  (cond ((= kinds-of-coins 1) 1)
        ((= kinds-of-coins 2) 5)
        ((= kinds-of-coins 3) 10)
        ((= kinds-of-coins 4) 25)
        ((= kinds-of-coins 5) 50)))

So count-change takes an amount and passes that amount to the cc procedure. It also initializes the "kinds-of-coins" value to "5".

cc implements the core logic of the program.

(= amount 0) 1)

If an amount is reached that is exactly 0, that indicates that a coin sequence was attempted and no change was left over, which indicates that change was validly made. We therefore want to count that as 1 valid way to make change.

(or (< amount 0) (= kinds-of-coins 0)) 0)

First let's think about (< amount 0). Consider what having a negative amount would mean. Suppose we wanted to make change on 30 cents using quarters, dimes, or nickels. 1 quarter + 1 nickel is a valid solution. OTOH, what would happen if we tried 2 quarters? We'd wind up with -20 cents. So we want to catch that case and not count it as a valid way of making change.

Next consider (= kinds-of-coins 0)) 0). This happens when we run out of coins but our amount isn't 0 or less than zero. Suppose, for example, that we were trying to make change of 33 cents using only dimes and nickels as our denominations. You can't actually do that, so we want to return 0 ultimately. But our procedure needs to verify that we can't actually do this, and try various possibilities like 3 dimes, 2 dimes and 2 nickels, whatever. In all those cases, we'll ultimately get to a point where there are 3 cents left over as the amount. So we need something to cover the case where the amount is greater than 0 but all the available coins have been tried.

The else clause has a lot going on:

(else (+ (cc amount
                     (- kinds-of-coins 1))
                 (cc (- amount
                        (first-denomination kinds-of-coins))
                     kinds-of-coins)))))

So the + is adding up the results of the lower level calculations - all the 1's and 0's that are getting returned depending on whether or not the coin sequence is valid.

(cc amount (- kinds-of-coins 1)) represents "the number of ways to change amount a using all but the first kind of coin." The reduction by 1 of kinds-of-coins serves to remove the current highest denomination coin from consideration in that recursive call to cc.

(cc (- amount (first-denomination kinds-of-coins)) kinds-of-coins) represents "the number of ways to change amount $a−d$ using all n kinds of coins, where d is the denomination of the first kind of coin." The first-denomination subprocedure serves to turn the value of the current kinds-of-coins into a specific value of currency which can be subtracted from amount.

first-denomination is straightforward. They do have an important comment on it in the book though:

Here we are thinking of the coins as arranged in order from largest to smallest, but any order would do as well.

Initially I thought that if you wanted a different order, like smallest to largest, you'd need to rewrite various parts of the program. But I think the first-denomination part may stand on its own in letting you reverse the order. I tried this variation on that subprocedure:

(define (first-denomination kinds-of-coins)
  (cond ((= kinds-of-coins 1) 50)
        ((= kinds-of-coins 2) 25)
        ((= kinds-of-coins 3) 10)
        ((= kinds-of-coins 4) 5)
        ((= kinds-of-coins 5) 1)))

And I got the same results for a couple of tests.

Exercises

Exercise 1.9 ✅

Each of the following two procedures defines a method for adding two positive integers in terms of the procedures inc, which increments its argument by 1, and dec, which decrements its argument by 1.

(define (+ a b)  (if (= a 0)       b       (inc (+ (dec a) b))))

(define (+ a b)
  (if (= a 0) 
      b 
      (+ (dec a) (inc b))))

Using the substitution model, illustrate the process generated by each procedure in evaluating (+ 4 5). Are these processes iterative or recursive?

The first procedure is definitely recursive (and very similar to an example discussed in The Little Schemer IIRC). Basically, it uses inc to build up a deferred chain of operations that add 1 while at the same time invoking itself with a value of a reduced by 1, until a is 0. At that point, we stop deferring the operations. We return whatever initial value b had, and then add the deferred additions of 1 to that b value as it "percolates" back up the chain of recursive calls.

Here's an illustration of how this version of + works with the arguments 3 and 4:

(+ 3 4)
(+ 1 (+ 2 4))
(+ 1 (+ 1 (+ 1 4)))
(+ 1 (+ 1 (+ 1 (+ 0 4))))
(+ 1 (+ 1 (+ 1 4)))
(+ 1 (+ 1 5))
(+ 1 6)
7

And the output we see running a trace on + in DrRacket is compatible with this:

The second procedure is iterative. There's no build up of a deferred chain of operations, and the state at which we are in the computational process is fully captured by the a and b variables. The way it works, basically, is a recursive call is made with a decreased and b increased until a equals 0. At that point, b, which has been getting incremented with each iterative step, is returned as the value of the procedure.

Exercise 1.10 ✅

The following procedure computes a mathematical function called Ackermann's function.

(define (A x y)
  (cond ((= y 0) 0)
        ((= x 0) (* 2 y))
        ((= y 1) 2)
        (else (A (- x 1)
                 (A x (- y 1))))))

The Values of Particular Expressions

What are the values of the following expressions?

(A 1 10)
(A 2 4)
(A 3 3)

The exercise only asks for the values, which could be determined just by running the program, but I wanted to try to figure out what was actually going on.

First, (A 10)

I made a diagram of some of the operation of (A 1 10) to help understand what was happening:

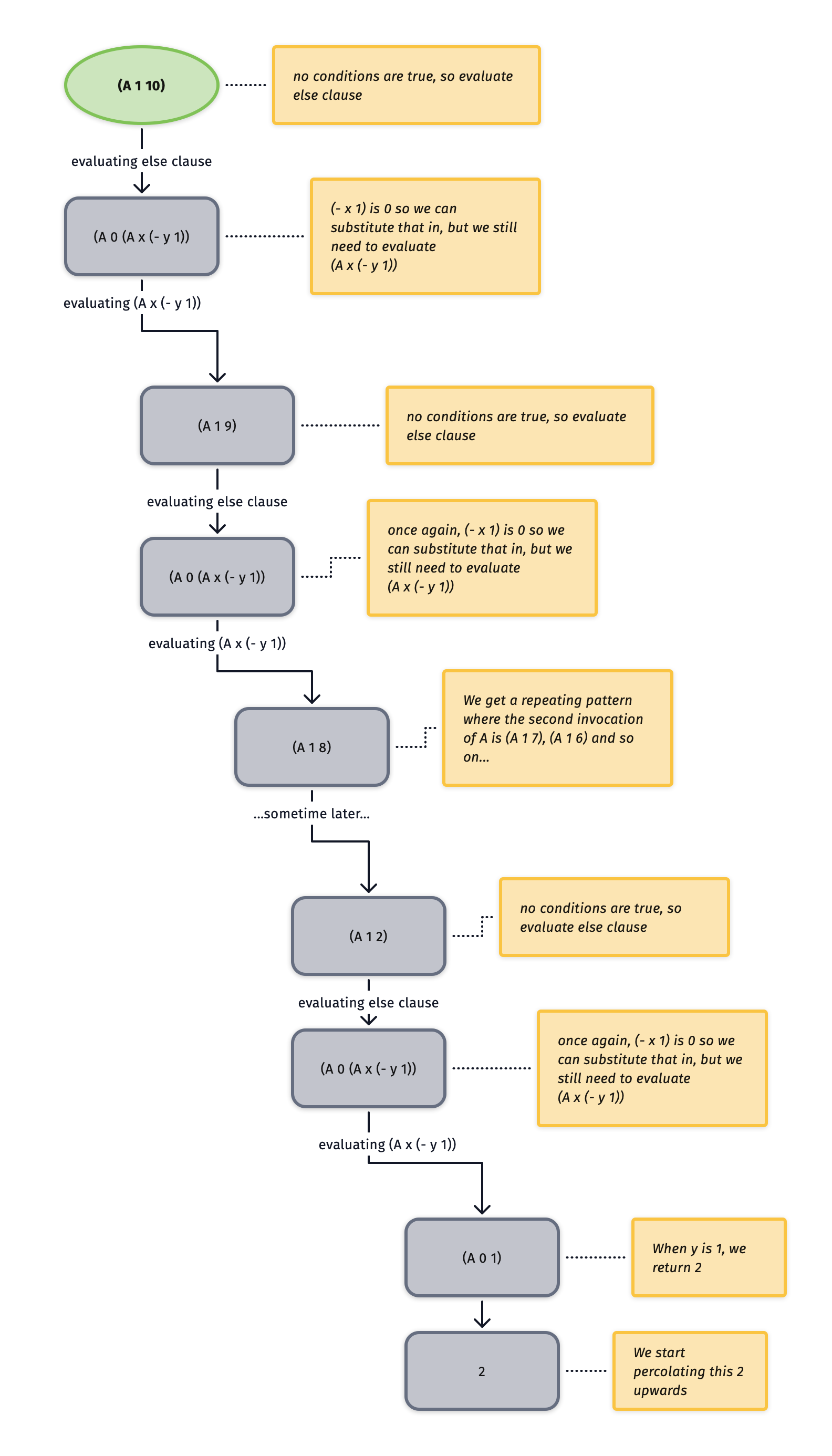
So my diagram captures some of the "downward" process but there's also the steps back up. As the 2 we got from evaluating the situation when y = 1 percolates back up, it's going to run into a bunch of deferred calculations where x = 0 and the A procedure is waiting on a y value. For each of those instances, we're going to multiply y by 2. Since we start at the "bottom" of our chain of recursive calls with a value of 2 for (A 0 1) and we started with (A 1 10), I'm guessing we're gonna wind up with like 1024? Might be an off by one error though, or maybe I misunderstood something. Let's check the interpreter.

🙂

Basically btw, if the first value to A is 1, then you basically $2^x$ where $x$ is the second value to A.

Next, let us consider (A 2 4). I made a Mindnode graph for this one:

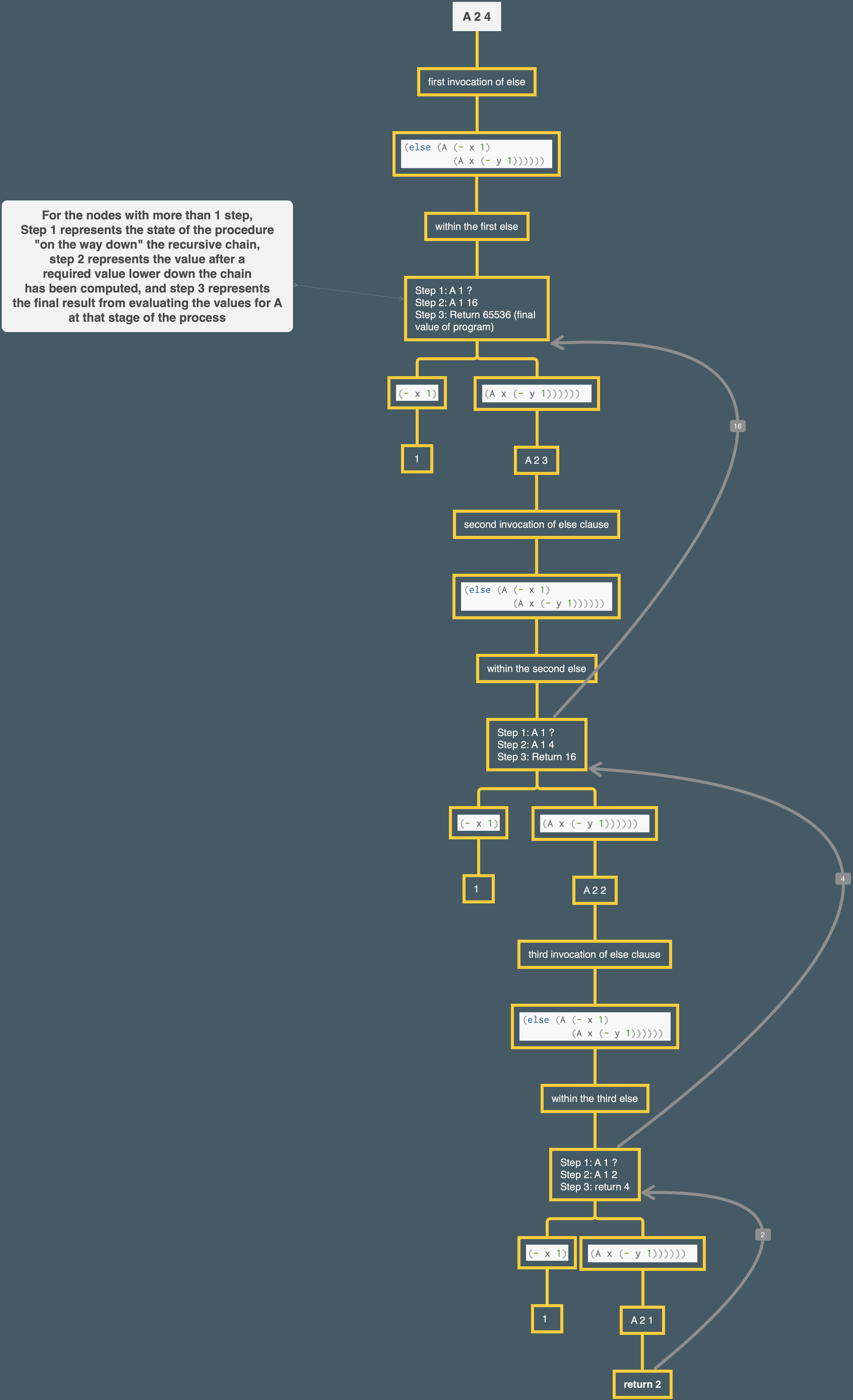
The graph was helpful for troubleshooting. Initially I was intuitively expecting the same result as with (A 1 x) and calculated the result to be 16. Way off, LOL!

So here's the essential difference between an (A 1 x) statement and an (A 2 x) statement. With (A 1 x), e.g. (A 1 10), because of how the procedure operates, we were building up a chain of deferred (A 0 x) operations. If the first value is to A is 0, we multiply by 2. We had 10 steps of our chain, so we wound up with 1024.

With an (A 2 x) statement, like (A 2 4), we are building up a chain of deferred (A 1 x) operations. So when we get down to the base case and start percolating the values back up, we aren't multiplying those values by 2. Instead, those values become the power to which we raise 2. This makes a big difference, which you can tell from the speed with which (A 2 x) starts to take off at (A 2 4) (and if you try (A 2 5) it may take your computer a while!)

BTW to understand my graph for (A 2 4), I think it's best to at that point just treat (A 1 x) as "a procedure which returns the power of 2 raised to the $x$ power" and not break it down more than that. Gets too messy otherwise.

Ok now

(A 3 3)

This returns 65536 also. We see that (A 3 x) goes up even faster than (A 2 x):

I think this is because the chain of deferred operations within (A 3 x) involves taking the value that's returned when reaching the base case and percolating it up through (A 2 x)'s. And we know what the value of (A 2 4) is!

Concise Mathematical Definitions

Consider the following procedures, where A is the procedure defined above:

(define (f n) (A 0 n))
(define (g n) (A 1 n))
(define (h n) (A 2 n))
(define (k n) (* 5 n n))

Give concise mathematical definitions for the functions computed by the procedures f, g, and h for positive integer values of n. For example, (k n) computes $5n^2$

f is $2 \times n$

g is $2^n$

h is ${^{n}2}$ (explained below)

While I think that f and g follow pretty naturally from what I discussed above, I was stuck on h for a while. I tried to guess various functions to "fit" the values returned for plugging in different values for n but none of them fit. . I was about to give up, but then I decided to just start writing ay facts I knew about the values returned by the function. E.g. for (A 2 3) I wrote down that the value returned by that could be expressed as $2^4$, or $4^2$, or $2^{2^{2}}$

So then I realized the following:

(A 2 1) = 2

(A 2 2) = 4 = $2^2$

(A 2 3) = 16 = $2^{2^{2}}$

(A 2 4) = 65536 = $2^{2^{2^{2}}}$

(Note I've been through some of the SICP material before, so my memory was probably jogged a bit here - I am not just discovering this for the first time).

Wikipedia has an article on this kind of operation, which is apparently called "tetration". The part on the order of evaluation is simple and clear (you start at the deepest level of the tower of exponents and work your way out. They have a simple and clear example).

Since I figured out what was happening conceptually, I'm not gonna ding myself for not knowing notation for estoeric math offhand given that I'm not part of the intended audience of MIT CS students who were reading SICP back in the day :)

As far as notation, Wikipedia has a bunch https://en.wikipedia.org/wiki/Tetration#Notation

I went with the "Rudy Rucker" notation for the concise mathematical definition cuz I found it simple and it was easy to do in MathJax (I did ${^{n}2}$ if you care).

Unanswered Questions

What exactly was the relevance of the golden ratio in understanding the inefficiency of the recursive fibonacci procedure? Quote of relevant material:

In fact, it is not hard to show that the number of times the procedure will compute (fib 1) or (fib 0) (the number of leaves in the above tree, in general) is precisely Fib(n + 1). To get an idea of how bad this is, one can show that the value of Fib(n) grows exponentially with n. More precisely (see exercise 1.13), Fib(n) is the closest integer to $\phi^n/\sqrt{5}$ , where

$$\phi = (1 + \sqrt{5})/2 \approx 1.6180 $$

is the golden ratio, which satisfies the equation

$$\phi^2 = \phi + 1$$