Peikoff Homework/Classwork on Immediate Inference and Categorical Syllogisms
More Peikoff Logic Homework
Table of Contents
The following consists of my answers for one of the homework sets in Leonard Peikoff's Introduction to Logic course. The handout with the exercises is freely available on the Ayn Rand Institute's website for the course. These exercises start on page 9 in the handout.
I used ✅ where I and Peikoff agreed and ❌ where I got a different answer and agreed with Peikoff's reasoning at the end of the day. I used 🤔 when I wasn't sure how to proceed and just listened to Peikoff's discussion. For some questions I may use multiple emoji and the reason why should be clear upon reading my answer.
These problems deal with Immediate Inference and Categorical Syllogisms. My answers below assume familiarity with the background concepts and won't make sense if you don't have the relevant background knowledge.
Immediate Inference
Problem 1
1. Given that the statement “All thinkers are doers” is TRUE, state whether each of the following is True, False, or Undetermined:
Part a ✅
a. Some non-doers are not non-thinkers.
So we're given a statement, "All Thinkers are Doers" that we could represent as "All S is P" (with S representing the thinkers and P representing the doers). I will use that representation consistently throughout. Then we're given something we can represent as "Some non-P are not non-S."
"Some non-P are not non-S." is the obverse of "Some non-P are S."
"Some non-P are S" is the converse of "Some S are non-P." (ok so far I think)
"Some S are non-P." is the contradictory of "All S is P."
Therefore, “All thinkers are doers” being true implies that "Some non-doers are not non-thinkers" is false.
Put differently: "Some non-doers are not non-thinkers" means the same thing as "Some non-doers are thinkers." But if “All thinkers are doers”, then every single thinker has to be in the set of doers, which means no thinkers can be in the set of non-doers. This means that no non-doers are thinkers.
Peikoff proceeded in a different manner: starting from "All S is P", he took the contrapositive, getting "All non-P is non-S."
He then identified "Some non-P are not non-S." as the contradictory of the contrapositive.
Part b ✅
b. No doers are non-thinkers.
This would be "No P are non-S." This is the obverse of "All P are S." Assuming the truth of "All S are P", the status of "All P are S" is undetermined, since we can't say whether or not "All P are S" from the truth of "All S are P". "All P are S" could be true, if the sets of S and P perfectly over lap, but it might not be true. So the answer here is undetermined.
Part c ❌
First Attempt (ERROR) ❌
c. No non-thinkers are non-doers.
This would be "No non-S are non-P."
(the following is wrong)
❌ If we take the contrapositive, it's "No P are S", or "No doers are thinkers".
❌ Our premise is "All S is P", or “All thinkers are doers”. If every thinker is a doer, then assuming there are any thinkers at all, some of the doers must be thinkers. So "No non-S are non-P." is false.
❌Another way: we said that the contrapositive of "No non-S are non-P." is "No P are S". The converse of that is "No S are P." So we have "No S are P" against "All S is P". Since we have accepted "All S is P" as true, the statement that produces "No S are P" has to be false.
Post-Mortem 🧐
I somehow wasn't aware of the limited scope of contrapositive statements. I don't think Peikoff made this particularly clear in the lecture, but I'm not 100% sure.
Only the contrapositive of "A" (e.g. All S is P) and "O" (e.g. Some S is not P) statements can be taken. "No non-S are non-P." is an "E" type proposition. Why can't you take the contrapositive of an "E" type statement? Taking the contrapositive can be broken into three steps: taking the obverse, taking the converse, and taking the obverse again. On an E type statement, if you take the obverse, you go from "No S is P" to "All S is non-P." This is an A type statement. At this point, you need to take the converse to continue finding the contrapositive. You cannot take the converse of an A statement, however. You can do something called "converse by limitation", but this loses information. E.g. you can go from "All men are mortal" to "some mortals are men." But in the "All men are mortal" form, we had information about every man. We lose this information in the "converse by limitation", since we only know stuff about some men now. Similar is true for I type statements ("Some S are not P.").
I statements ("Some S is not P") also cannot have their contrapositive taken. If you take the obverse of "Some S is not P", then you change the "is not" to "is" and the "P" to "non-P", resulting in "Some S is non-P.". This as the same truth value as the original statement; it's still an I proposition. I statements don't have a converse.
Second Attempt ✅
"No non-S are non-P."
I got a hint from Peikoff before pausing the video to write my post-mortem, which was to take the contrapositive of our original given premise, "All S is P." This would be "All non-P is non-S." We could further obvert this, which gives us "No non-P is S".
We can take the converse of "No non-S are non-P", which is "No non-P are non-S." The contradiction is clear, and thus "No non-S are non-P." has to be false.
Peikoff notes that "No non-S are non-P." is the contrary of "All non-P is non-S."
Part d ✅
d. All non-thinkers are non-doers.
This would be "All non-S are non-P." Contrapositive is "All P is S."
What is the relationship to "All S is P"?
It's undetermined. We can't say whether or not "All P is S." from knowing "All S is P."
If the sets of S and P perfectly overlap, then it could be true that "All P is S." OTOH, if S is a subset of P, then there could be some Ps that are non-S.
Peikoff takes the contrapositive of the original statement instead, getting All Non-P is Non-S. The relationship between All Non-P is Non-S and All non-S are non-P is that one is the simple converse of the other. But the simple converse of an A type statement is undetermined.
Problem 2
Given that the statement “No mortals are happy” is FALSE, state whether each of the following is True, False, or Undetermined:
We will represent the false statement “No mortals are happy” as "No S is P."
Part a ✅
a. All mortals are unhappy.
We will represent the statement "All mortals are unhappy" as "All S is non-P."
"All S is non-P" is merely the obverse of "No S is P."
Since "No S is P." is false, "All S is non-P" is also false.
Part b ✅
b. All mortals are happy.
We will represent the statement "All mortals are happy." as "All S is P."
"No S is P" is the contrary of "All S is P." Contraries are statements where the truth of one implies the falsehood of the other, but the falsehood of one does not imply the truth of the other. So the truth of "All S is P." is undetermined.
Putting it differently: if we know that No S is P is false, then we know that at least Some S is P, but we don't know how much (whether it's just Some or whether All S is P). So the truth of All S is P is undetermined. Like if we had the statements "No Americans live in Mexico", and we say that that statement is false, then we know that there is at least one American living in Mexico, but we don't know whether we're talking about some Americans living in Mexico or all Americans.
Part c ✅
c. All happy beings are immortal.
We will represent the statement "All happy beings are immortal." as "All P are non-S."
The obverse of this statement is "No P are S."
The converse of this statement is "No S is P".
Since "No S is P" is false, "All happy beings are immortal." is also false.
Part d ✅
d. Some happy beings are not immortal.
We will represent the statement "Some happy beings are not immortal." as "Some P are not non-S."
The obverse of this statement is "Some P is S".
The converse of this statement is "Some S is P."
"Some S is P" is the contradictory of "No S are P." Since "No S are P." is false, "Some S is P" is true.
Categorical Syllogisms
Problem 2 ✅
All materialists are atheists. All communists are atheists. So all materialists are communists.
Identify the Components
Premise: All materialists are atheists.
Premise: All communists are atheists.
Conclusion: So, all materialists are communists.
Middle term: atheists.
Minor term: materialists.
Major term: communists.
Analyze
The syllogism only has 3 terms and thus does not commit the Fallacy of Four Terms.
The middle term is not distributed. We know that all communists are within the set of atheists, and we know that all materialists are within the set of atheists. But we do not know something about every atheist. So this commits the Fallacy of the Undistributed Middle. It is invalid.
Problem 3 ✅
All dictators use propaganda. No mathematician uses propaganda. Hence, no mathematician is a dictator.
Identify the Components
Premise: All dictators use propaganda.
Premise: No mathematician uses propaganda.
Conclusion: Hence, no mathematician is a dictator.
Middle term: (user of) propaganda.
Minor term: mathematician.
Major term: dictator.
Chart of Distributions
Note: Peikoff went with the very logical conversion of "use propaganda" into "propagandists", which I agree would have been better/clearer.
| Statement | Distribution of Subject | Distribution of Predicate |
|---|---|---|
| All dictators use propaganda | D | U |
| No mathematician uses propaganda. | D | D |
| Hence, no mathematician is a dictator. | D | D |
Analysis
The syllogism only has 3 terms and thus does not commit the Fallacy of Four Terms.
The middle term is distributed at least once and thus does not commit the Fallacy of the Undistributed Middle.
The terms that are distributed in the conclusion are likewise distributed in the premises, avoiding the Fallacy of the Illicit Minor and Major.
Only one of the premises is negative, avoiding the Fallacy of Two Negatives.
Given that one of the premises is negative, the conclusion is negative, avoiding the unnamed fallacy.
The argument is valid.
Problem 4 ✅
Since all intelligent men are creative, and all who are creative hold patents, it follows that all who hold patents are intelligent.
Identify the Components
Premise: all intelligent men are creative men
Premise: all creative men are patentholders
Conclusion: it follows that all patentholders are intelligent men
Middle Term: creative men
Minor Term: patentholders
Major Term: intelligent men
Chart of Distributions
| Statement | Distribution of Subject | Distribution of Predicate |
|---|---|---|
| all intelligent men are creative men | D | U |
| all creative men are patentholders | D | U |
| It follows that all patentholders are intelligent men | D | U |
Analysis
Does the syllogism have only 3 terms?
Yes.
Is the middle term distributed at least once?
Yes.
Are terms that are distributed in the conclusion also distributed in the premises?
No! Patentholders is not distributed in the premise. (Fallacy of Illicit Minor).
The argument is invalid.
Another way of analyzing: we know that all intelligent men are in the set of creative men, and we know that all creative men are in the set of patent holders. So we can say that all intelligent men are patent holders. But we can't go the other way. There could be plenty of patentholders that are uncreative based on our premises, and plenty of creative men that are unintelligent as well, and therefore, plenty of patentholders that are unintelligent. The following crude graphic depicts one possible relationship of the groups based on the premises:
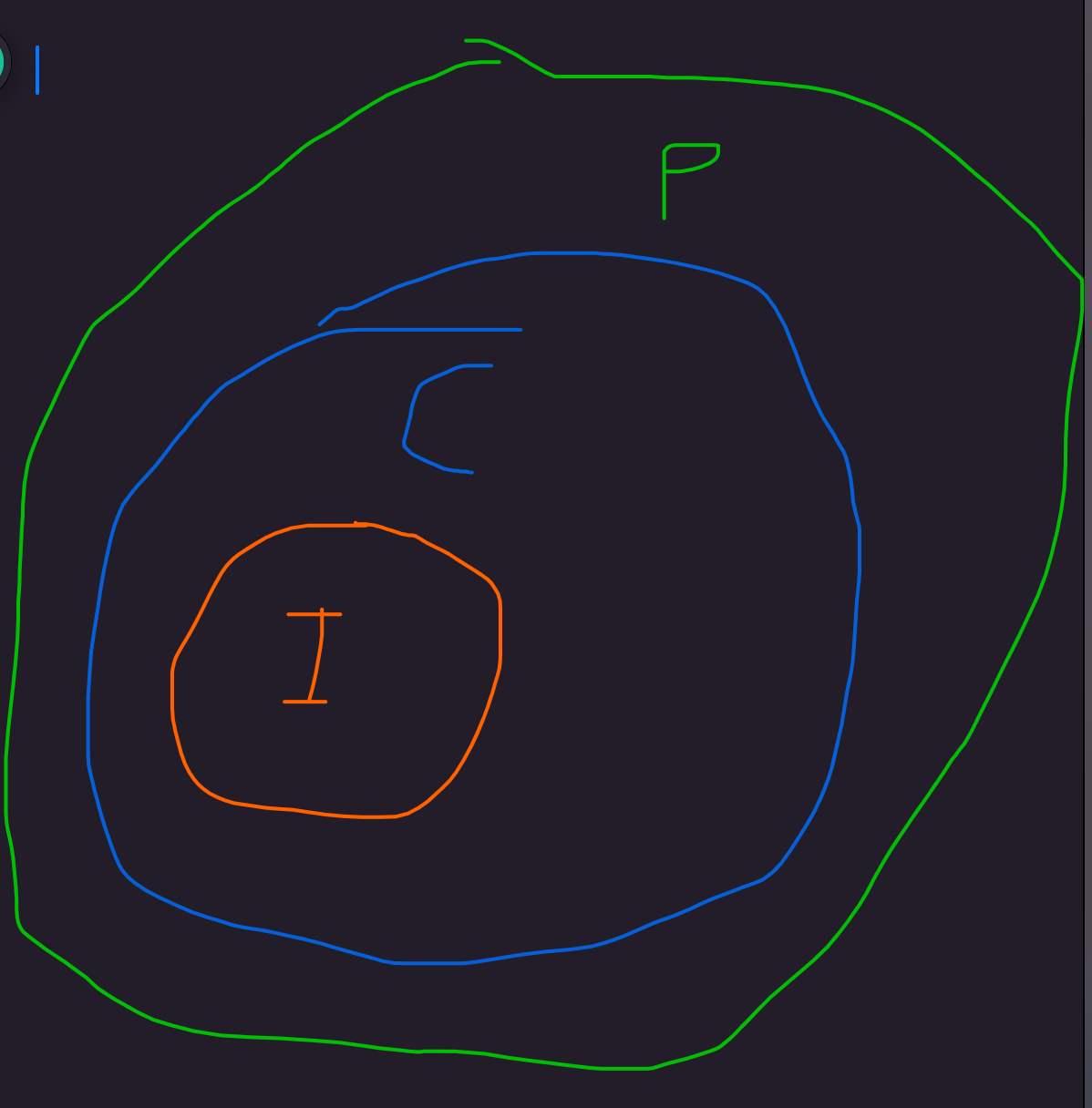
Problem 5 ✅
All conventional people are unhappy. All innovators are unconventional. Therefore, no innovators are unhappy.
Identify the Components
Premise: All conventional people are unhappy
Premise: All innovators are unconventional
Conclusion: Therefore, no innovators are unhappy
Take the Obversion
We need to take the obversion of a premise in order to get to 3 terms.
All innovators are unconventional --> No innovators are conventional.
Now we have
Finish Identifying the Components
Premise: All conventional people are unhappy
Premise: No innovators are conventional
Conclusion: Therefore, no innovators are unhappy
Middle Term: conventional (people)
Minor Term: innovators
Major Term: unhappy
Chart of Distributions
| Statement | Distribution of Subject | Distribution of Predicate |
|---|---|---|
| All conventional people are unhappy | D | U |
| No innovators are conventional | D | D |
| Therefore, no innovators are unhappy | D | D |
Analysis
Does the syllogism have only 3 terms?
Yes.
Is the middle term distributed at least once?
Yes.
Are terms that are distributed the conclusion also distributed in the premises?
No. Unhappy is undistributed in the premise. This is the fallacy of illicit major.
The argument is invalid.
Here is a crude graphic depicting a result compatible with the first two premises but contradicting the third:
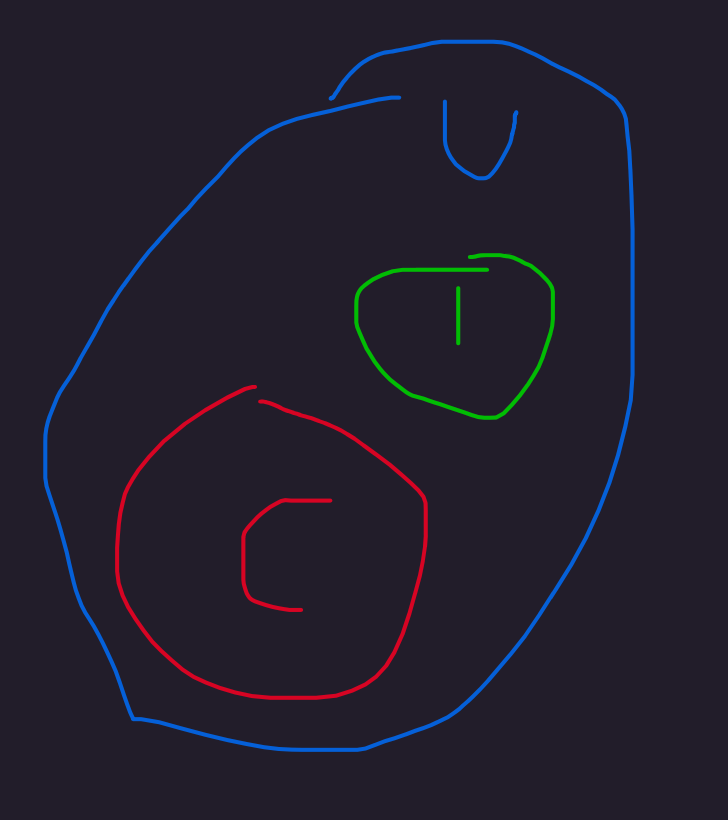
Problem 6 ✅
Some attractive people are not lacking in energy, and all unpopular people are unattractive. Thus, some energetic people are popular.
Identify the Components
Premise: Some attractive people are not lacking in energy
Premise: all unpopular people are unattractive
Conclusion: Thus, some energetic people are popular
I think we can reword "Some attractive people are not lacking in energy" to "Some attractive people are energetic". (Note: what I thought of as just getting rid of a double negation, Peikoff approached as taking the obverse of this premise.)
Making the second premise useful, however, requires another step: taking the contrapositive.
all unpopular people are unattractive -> All attractive people are popular.
So now we have:
Some attractive people are energetic.
All attractive people are popular.
Thus, some energetic people are popular.
Middle Term: attractive people.
Minor Term: energetic people.
Major Term: popular (people).
Chart of Distributions
| Statement | Distribution of Subject | Distribution of Predicate |
|---|---|---|
| Some attractive people are energetic. | U | U |
| All attractive people are popular. | D | U |
| Thus, some energetic people are popular. | U | U |
Analysis
Does the syllogism have only 3 terms?
Yes.
Is the middle term distributed at least once?
Yes.
Are terms that are distributed the conclusion also distributed in the premises?
Yes (there are no terms distributed in the conclusion).
Is no more than one of the premises negative?
Yes (none are).
Is one of the premises negative? Then the conclusion must be negative.
N/A.
Is the conclusion negative? Then one premise must be negative.
N/A.
The argument is valid.
Intuitive analysis: we know that every single attractive person is one of the popular people. We know that some of those attractive people (all of whom, again, are popular) are energetic. So some energetic people are popular (and indeed, the ones we know something about must also be attractive people).
Another crude diagram:
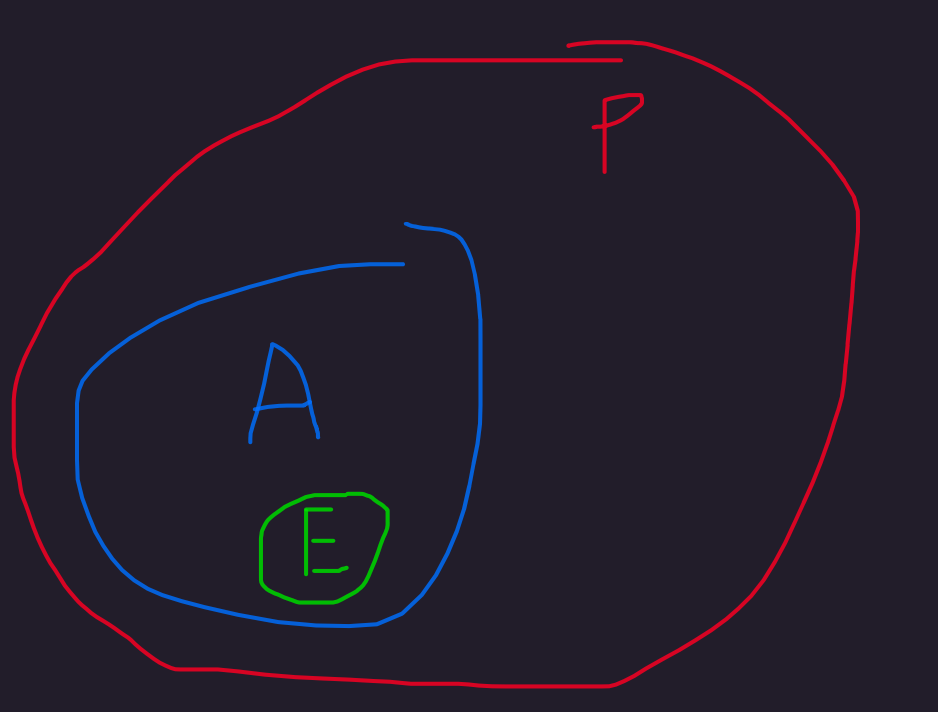
Problem 7 ✅
People who deceive themselves are not students of logic. My proof of this is that most self-deceivers rationalize a great deal, and logic students never rationalize.
Identify the Components
Premise: most self-deceivers rationalize a great deal
Premise: logic students never rationalize
Conclusion: People who deceive themselves are not students of logic
And putting it in a more standard form:
Premise: Some self-deceivers are rationalizers
Premise: No logic students are rationalizers
Conclusion: Therefore, no self-deceivers are logic students
Middle Term: rationalizers
Minor Term: self-deceivers
Major Term: logic students
Chart of Distributions
| Statement | Distribution of Subject | Distribution of Predicate |
|---|---|---|
| Some self-deceivers are rationalizers | U | U |
| No logic students are rationalizers | D | D |
| Therefore, no self-deceivers are logic students | D | D |
Analysis
Does the syllogism have only 3 terms?
Yes.
Is the middle term distributed at least once?
Yes.
Are terms that are distributed the conclusion also distributed in the premises?
No. The minor term, "self-deceivers", is not distributed. This is the fallacy of illicit minor.
Intuitive explanation: If we know that "some self-deceivers are rationalizers", then it could be the case that some self-deceivers are not rationalizers. Therefore, we can't deduce from the additional fact that "No logic students are rationalizers" that "no self-deceivers are logic students". This is because some non-rationalizing self-deceivers could still be logic students.
Problem 8 ✅
Samuel Johnson, Life of Cowley: “Because the father of poetry was right in denominating poetry . . . an imitative art, these [metaphysical poets] will, without great wrong, lose their right to the name of poets . . . for they copied neither nature nor life.”
Identify the Components
the father of poetry was right in denominating poetry . . . an imitative art
these [metaphysical poets] will, without great wrong, lose their right to the name of poets
for they copied neither nature nor life
Premise: the father of poetry was right in denominating poetry . . . an imitative art
Premise: for they copied neither nature nor life
Conclusion: these [metaphysical poets] will, without great wrong, lose their right to the name of poets
and in more standard form
Premise: All poets are imitative (or "All poetry is imitative")
Premise: No metaphysical poets are imitative. (or "No metaphysical poetry is imitative")
Conclusion: No metaphysical poets are poets. (or "No metaphysical poetry is poetry").
Middle Term: Imitative.
Minor Term: Metaphysical poets.
Major Term: Poets.
Chart of Distributions
| Statement | Distribution of Subject | Distribution of Predicate |
|---|---|---|
| All poets are imitative | D | U |
| No metaphysical poets are imitative | D | D |
| No metaphysical poets are poets | D | D |
Analysis
Does the syllogism have only 3 terms?
Yes.
Is the middle term distributed at least once?
Yes.
Are terms that are distributed the conclusion also distributed in the premises?
Yes.
Is no more than one of the premises negative?
Yes.
Is one of the premises negative? Then the conclusion must be negative.
This is the case.
Is the conclusion negative? Then one premise must be negative.
This is the case.
The argument is valid 🎊
Problem 9 ✅
Whatever is endorsed by science is objectively real. ESP, therefore, is obviously unreal, since it has no scientific credentials at all.
Identify the Components
Premise: Whatever is endorsed by science is objectively real
Premise: ESP has no scientific credentials at all
Conclusion: ESP, therefore, is obviously unreal
And in standard format:
Premise: All science-approved things are real.
Premise: No ESP is science-approved.
Conclusion: No ESP is real.
Middle Term: Science-approved.
Minor Term: ESP.
Major Term: Real.
Chart of Distributions
| Statement | Distribution of Subject | Distribution of Predicate |
|---|---|---|
| All science-approved things are real. | D | U |
| No ESP is science-approved. | D | D |
| No ESP is real. | D | D |
Analysis
Does the syllogism have only 3 terms?
Yes.
Is the middle term distributed at least once?
Yes.
Are terms that are distributed the conclusion also distributed in the premises?
No. The term "real" is not distributed in the premises. This is the Fallacy of Illicit Major.
Intuitive explanation (and keep in mind this is only analyzing the logic): Just because all science-approved things are real, that doesn't mean that science-approved things are the only real things. There could be lots of stuff, like ESP, that is not science-approved, but is still real.
Problem 10 ✅
Those who eat a lot, gain weight; those who eat little, suffer; hence, those who gain weight do not suffer.
Identify the Components
Premise: Those who eat a lot, gain weight.
Premise: those who eat little, suffer.
Conclusion: hence, those who gain weight do not suffer.
And in standard form:
Premise: All heavy eaters are gainers.
Premise: All non-heavy eaters are sufferers.
Conclusion: No gainers are sufferers.
and reducing to three terms:
First we manipulate the second premise:
All non-heavy eaters are sufferers.
Obverse: No non-heavy-eaters are non-sufferers.
Converse: No non-sufferers are non-heavy-eaters.
Obverse: All non-sufferers are heavy eaters.
Then we manipulate the conclusion:
No gainers are sufferers.
Obversion: All gainers are non-sufferers.
And now our three terms are:
Premise: All heavy eaters are gainers. (Peikoff had, using my terminology: All non-gainers are non-heavy-eaters.)
Premise: All non-sufferers are heavy eaters. (Peikoff had, using my terminology: All non-heavy eaters are sufferers).
Conclusion: All gainers are non-sufferers. (Peikoff had, using my terminology: All sufferers are non-gainers.)
Middle Term: heavy eaters
Minor Term: gainers
Major Term: non-sufferers
Chart of Distributions
| Statement | Distribution of Subject | Distribution of Predicate |
|---|---|---|
| All heavy eaters are gainers. | D | U |
| All non-sufferers are heavy eaters. | D | U |
| Conclusion: All gainers are non-sufferers. | D | U |
Analysis
Does the syllogism have only 3 terms?
Yes.
Is the middle term distributed at least once?
Yes.
Are terms that are distributed the conclusion also distributed in the premises?
No. "Gainers" is not distributed. This is Fallacy of Illicit Minor.
Analysis: We know that every non-sufferer is in the set of heavy eaters. And we know that every heavy eater is in the set of gainers. From that, we can validly infer that every non-sufferer is a gainer. We can't go the other way, though, like the argument wants us to, because there might be gainers who are not heavy eaters.
Another crude graphic depicting a possible set of relationship based on the premises (and which contradicts the conclusion):
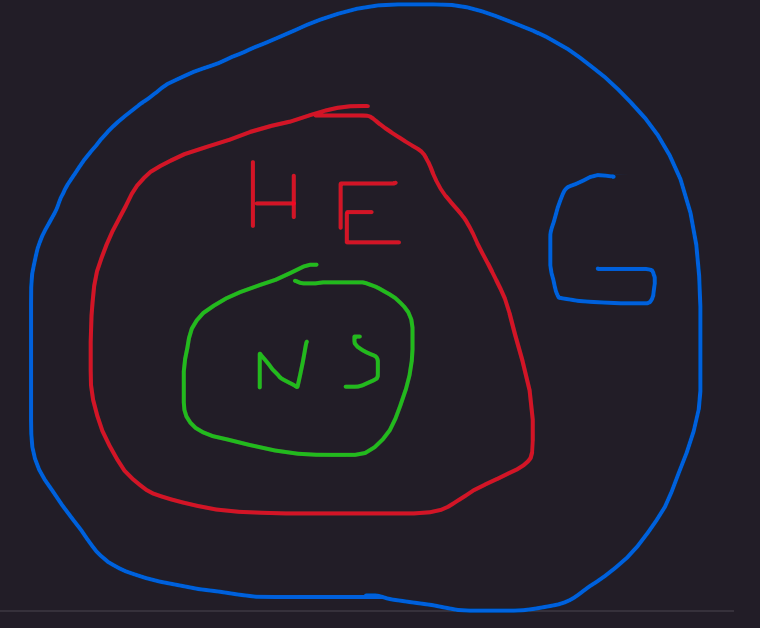
Problem 11 ✅
First Argument
Everyone except for ecologists is concerned about the energy crisis. So Professor Smith, an avid ecologist, is not concerned about it.
Identify the Components
Premise: No ecologists are concerned (about the energy crisis).
(Another premise that we can get is: "All non-ecologists are concerned." My initial idea is that it was unnecessary to analyze this, as it wasn't the point of the argument, but Peikoff said to analyze it, so I tried that below).
Premise: All Professor Smith is an ecologist.
Conclusion: No Professor Smith is concerned.
Middle Term: Ecologists.
Minor Term: Professor Smith.
Major Term: concerned.
Chart of Distributions
| Statement | Distribution of Subject | Distribution of Predicate |
|---|---|---|
| No ecologists are concerned. | D | D |
| All Professor Smith is an ecologist. | D | U |
| No Professor Smith is concerned. | D | D |
Analysis
Does the syllogism have only 3 terms?
Yes.
Is the middle term distributed at least once?
Yes.
Are terms that are distributed the conclusion also distributed in the premises?
Yes.
Is no more than one of the premises negative?
Yes.
Is one of the premises negative? Then the conclusion must be negative.
Yes, this is the case.
Is the conclusion negative? Then one premise must be negative.
Yes, this is the case.
The argument is valid 🎊
Second Argument
Identify the Components
Premise: All non-ecologists are concerned.
Premise: All Professor Smith is an ecologist.
Conclusion: No Professor Smith is concerned.
We need to manipulate "All non-ecologists are concerned." into something useful.
How about the contrapositive? "All those non-concerned are ecologists."
We can manipulate the conclusion "No Professor Smith is concerned" too.
Obverse: "All Professor Smith are non-concerned."
(Peikoff instead converted the second premise to "No Professor Smith is non-ecologist." On his approach, he came up with a different fallacy: Illicit Major. I checked this and confirmed it myself. I thought it was interesting how the fallacy you discover can vary with how you translate things.)
Now our setup is:
Premise: All those non-concerned are ecologists.
Premise: All Professor Smith is an ecologist.
Conclusion: All Professor Smith are non-concerned.
Middle Term: ecologists.
Minor Term: Professor Smith
Major Term: non-concerned.
Chart of Distributions
| Statement | Distribution of Subject | Distribution of Predicate |
|---|---|---|
| All those non-concerned are ecologists.. | D | U |
| All Professor Smith is an ecologist. | D | U |
| All Professor Smith are non-concerned. | D | U |
Analysis
Does the syllogism have only 3 terms?
Yes.
Is the middle term distributed at least once?
No.
The argument is invalid. But the original/overall argument is valid. "All non-ecologists are concerned" turned out to be an optional/inessential detail that doesn't detract from the valid argument we can get out of the original statement.
Problem 12 ✅❌
Only chronic liars meet nothing but failure in life. And we know that all chronic liars are unintelligent. It follows that none of the people who meet only failure in life are intelligent.
Identify the Components
Premise: Only chronic liars meet nothing but failure in life.
Premise: And we know that all chronic liars are unintelligent.
Conclusion: It follows that none of the people who meet only failure in life are intelligent.
❌ (ERROR)"Only chronic liars meet nothing but failure in life." means that the set of chronic liars and failures are overlapping. One way to represent this is by saying both "All chronic liars are failures" and "All failures are chronic liars". One way to approach this is to have two different sets of premise (one from each variant of the Only statement), as we did in the last section.
CORRECTION: I interpreted the "only" statement as being an IFF statement, meaning something like "If and only if one is a chronic liar will one meet failure in life." I then analyzed it in a manner similar to question 12. The statement was not intended as an IFF, and what Peikoff wanted was for you to reverse the only statement (as in "All failures are chronic liars".). Since I fully analyzed both statements, including the one I mistakenly read into the only statement, and I analyzed the one Peikoff intended correctly, I'm giving myself partial credit. I left my erroneous analysis below.
❌First Argument (ERROR - Erroneous analysis resulting from mistaken interpretation of one of the parts of the argument being analyzed)
In standard form:
Premise: All chronic liars are failures
Premise: All chronic liars are dumb.
Conclusion: No failures are non-dumb.
4 terms. Problem! One solution is to obvert the second premise
Premise: All chronic liars are dumb -> No chronic liars are non-dumb.
3 terms!
Premise: All chronic liars are failures
Premise: No chronic liars are non-dumb.
Conclusion: No failures are non-dumb.
Middle Term: chronic liars
Minor Term: failures
Major Term: non-dumb
| Statement | Distribution of Subject | Distribution of Predicate |
|---|---|---|
| All chronic liars are failures. | D | U |
| No chronic liars are non-dumb. | D | D |
| No failures are non-dumb. | D | D |
Analysis
Does the syllogism have only 3 terms?
Yes!
Is the middle term distributed at least once?
Yes.
Are terms that are distributed the conclusion also distributed in the premises?
Nope! "Failures" is not distributed in the premises. This is Fallacy of Illicit Minor.
✅Second Argument
Premise: All failures are chronic liars.
Premise: All chronic liars are dumb.
Conclusion: No failures are non-dumb.
4 terms. Again, we obvert the second premise
Premise: All chronic liars are dumb -> No chronic liars are non-dumb.
Premise: All failures are chronic liars.
Premise: No chronic liars are non-dumb.
Conclusion: No failures are non-dumb.
Middle Term: chronic liars
Minor Term: failures
Major Term: non-dumb
Chart of Distributions
| Statement | Distribution of Subject | Distribution of Predicate |
|---|---|---|
| All failures are chronic liars. | D | U |
| No chronic liars are non-dumb. | D | D |
| No failures are non-dumb. | D | D |
Analysis
Does the syllogism have only 3 terms?
Yes.
Is the middle term distributed at least once?
Yes.
Are terms that are distributed the conclusion also distributed in the premises?
Yes.
Is no more than one of the premises negative?
Yes.
Is one of the premises negative? Then the conclusion must be negative.
Yes, this is the case.
Is the conclusion negative? Then one premise must be negative.
Yes, this is the case.
The argument is valid 🎊.
Problem 13 ✅
There are a few men who cannot count to 20, and there are a great many men who have never been to college. So we may infer that some of the people who cannot count to 20 have never been to college.
Identify the Components
Premise: There are a few men who cannot count to 20
Premise: there are a great many men who have never been to college
Conclusion: some of the people who cannot count to 20 have never been to college
Standard form (with simplifications in language):
Premise: Some men are not numerate.
Premise: Some men are uneducated.
Conclusion: Some not numerate men are uneducated.
Middle Term: men
Minor Term: not numerate men
Major Term: uneducated
Chart of Distributions
| Statement | Distribution of Subject | Distribution of Predicate |
|---|---|---|
| Some men are not numerate. | U | U |
| Some men are uneducated. | U | U |
| Some not numerate men are uneducated. | U | U |
Analysis
Does the syllogism have only 3 terms?
Yes.
Is the middle term distributed at least once?
No. Fallacy of the undistributed middle.
Intuitively: The sets of innumerate and uneducated men don't need to overlap. They could be entirely separate.
Peikoff notes that if both premises are particulars ("some" statements), then no conclusion follows.
Problem 14 ✅
Bishop Berkeley, Three Dialogues Between Hylas and Philonous: “. . . intense heat is nothing else but a particular kind of painful sensation; and pain cannot exist but in a perceiving being; it follows that no intense heat can really exist in an unperceiving corporeal substance.”
Identify the Components
Premise: intense heat is nothing else but a particular kind of painful sensation
Premise: pain cannot exist but in a perceiving being
Conclusion: no intense heat can really exist in an unperceiving corporeal substance
Standard form (and with simplified language):
Premise: All intense heat is pain
Premise: All pain is in perceiving beings
Conclusion: No intense heat is in non-perceiving being.
Ok, we have too many terms. Let's change the second premise:
All pain is in perceiving beings -> No pain is in non-perceiving beings.
And now we have:
Premise: All intense heat is pain.
Premise: No pain is in non-perceiving beings.
Conclusion: No intense heat is in non-perceiving being.
Middle Term: pain
Minor Term: intense heat
Major Term: non-perceiving being
Chart of Distributions
| Statement | Distribution of Subject | Distribution of Predicate |
|---|---|---|
| All intense heat is pain. | D | U |
| No pain is in non-perceiving beings. | D | D |
| No intense heat in non-perceiving being. | D | D |
Analysis
Does the syllogism have only 3 terms?
Yes.
Is the middle term distributed at least once?
Yes.
Are terms that are distributed the conclusion also distributed in the premises?
Yes.
Is no more than one of the premises negative?
Yes.
Is one of the premises negative? Then the conclusion must be negative.
Yes, this is the case.
Is the conclusion negative? Then one premise must be negative.
Yes, this is the case.
The argument is valid.
Problem 15 ✅
If he didn’t cheat, why did he look so guilty when I asked him the question—which is just how cheaters always look in such circumstances.
Identify the Components
It was a bit tricky to tease out the argument here.
Premise: All cheaters look guilty.
Premise: All he looked guilty.
Conclusion: Therefore, all he is a cheater.
(Peikoff used "guilty-looker", as in "All cheaters are guilty-lookers").
Middle Term: Guilty
Minor Term: He
Major Term: cheater
Chart of Distributions
| Statement | Distribution of Subject | Distribution of Predicate |
|---|---|---|
| All cheaters look guilty. | D | U |
| All he looked guilty. | D | U |
| Therefore, all he is a cheater. | D | U |
Analysis
Does the syllogism have only 3 terms?
Yes.
Is the middle term distributed at least once?
No. This is the fallacy of the undistributed middle.
Problem 16 ❌
All the club members are not healthy. But some of them at least are not diabetics, because only unhealthy people have diabetes.
First Attempt ❌ ERROR
Premise: All club members are not healthy.
Error: I forgot that All S is not P is ambiguous and thus disallowed. (It could mean No S is P or Some S is Not P. We are to assume, if no information, that meaning is Some S is Not P)
Second attempt ❌ ERROR
For the "only" premise: only unhealthy people have diabetes = All diabetics are unhealthy = All non-unhealthy people are non-diabetic (or All healthy people are non-diabetic).
❌Following the analysis of the first error, I represent what was originally "All club members are not healthy" as "Some club members are unhealthy".
Middle Term: unhealthy/healthy
Minor Term: club members
Major Term: diabetics
❌Premise: Some club members are unhealthy.
Premise: All diabetics are unhealthy.
Conclusion: Some club members are not diabetics.
I treated the "not healthy" originally from "All the club members are not healthy" as equivalent to "unhealthy" without going through the necessary steps. I've been easy on myself about this up until now but have decided it's an error I'm going to be mindful of and take seriously going forward.
Third Attempt ✅
First Approach ✅
Premise: Some club members are not healthy.
Premise: All diabetics are unhealthy.
Conclusion: Some club members are not diabetics.
There are four terms here (healthy unhealthy, club members, and diabetics).
If we take the obverse of "Some club members are not healthy", we get "Some club members are non-healthy." I think it's fair to treat "non-healthy" and "unhealthy"as equivalent, so therefore...
Chart of Distributions
| Statement | Distribution of Subject | Distribution of Predicate |
|---|---|---|
| Some club members are unhealthy. | U | U |
| All diabetics are unhealthy. | D | U |
| Some club members are not diabetics. | U | D |
Analysis
Does the syllogism have only 3 terms?
Yes.
Is the middle term distributed at least once?
No. Fallacy of undistributed middle.
Second Approach ✅
If we instead obvert "All diabetics are unhealthy", we get "No diabetic is healthy." Let's analyze it that way too:
| Statement | Distribution of Subject | Distribution of Predicate |
|---|---|---|
| Some club members are not healthy. | U | D |
| No diabetic is healthy | D | D |
| Some club members are not diabetics. | U | D |
Analysis
Does the syllogism have only 3 terms?
Yes.
Is the middle term distributed at least once?
Yes.
Are terms that are distributed the conclusion also distributed in the premises?
Yes.
Is no more than one of the premises negative?
No! Fallacy of two negatives.
Problem 17 ✅
(Note that I heard Peikoff say the square of opposition was relevant to this question before answering it).
There is no basis for the view that all businessmen are materialists. And you must admit that if a person is a materialist, then he doesn’t believe in God. So you can’t claim that no businessmen are atheists.
Identify the Components
The first sentence claims that "all businessmen are materialists" is false. In the square of opposition, the "contradictory" of a given statement is the thing that is true if the given statement is false. Since "all businessmen are materialists" is an "All S is P" type statement, its contradictory is "Some S are not P", or, in our case, "Some businessmen are not materialists." Another way to get to the same place is to throw a "not" in our original statement that we are told is false. So we might phrase that as "All businessmen are not materialists". Given how we treat such statements by default, we get the result "Some businessmen are not materialists".
The second sentence says "if a person is a materialist, then he doesn’t believe in God." You could just go straight to "All materialists are atheists" but here's a more step by step approach:
That is most closely represented as "If a person is a materialist, then he is not a theist." Since we want a categorical statement, we could phrase this as "All materialists are not theists." This is "All S Is Not P", the case that we generally treat as ambiguous. I think in this case, it is clear that what is meant is that No S is P, or "No materialists are theists". This could be obverted to "All materialists are non-theists", or, just using a synonym, "All materialists are atheists".
The final sentence claims that "no businessmen are atheists" is false. This is a "No S is P" type statement. Its contradictory is "Some S are P", or, in our case, "Some businessmen are atheists."
So we have:
Premise: Some businessmen are not materialists.
Premise: All materialists are atheists.
Conclusion: Some businessmen are atheists.
Middle Term: materialists
Minor Term: businessmen
Major Term: atheists
Chart of Distributions
| Statement | Distribution of Subject | Distribution of Predicate |
|---|---|---|
| Some businessmen are not materialists. | U | D |
| All materialists are atheists. | D | U |
| Some businessmen are atheists. | U | U |
Analysis
Does the syllogism have only 3 terms?
Yes.
Is the middle term distributed at least once?
Yes.
Are terms that are distributed the conclusion also distributed in the premises?
Yes/NA.
Is no more than one of the premises negative?
Yes.
Is one of the premises negative? Then the conclusion must be negative.
Nope. Violation of Fifth Rule of Syllogistic Validity.
Problem 18 🤔
Schiller, Don Carlos: “King: That she was ardent-spirited—who can deny it? I could never give her love, yet—did she ever seem to feel the lack? Then it is proven, she is false.”
I had trouble figuring out what the premises were because of the language. I tried but could not get things down to less than four terms, so I listened to Peikoff a bit before starting my own analysis.
Peikoff says "did she ever seem to feel the lack?" means "She is indifferent." I don't follow.
Peikoff says this argument involves an implied premise (!).
So the first premise, per Peikoff, is something like "Al she is ardent, unloved by me, and indifferent." And the implied premise is "All people who are ardent, unloved by their husband, and indifferent are false." Therefore, she is false.
Identify the Components
Per Peikoff:
Premise: All she is a person who is ardent, unloved by her husband, and indifferent.
Implicit Premise: All persons who are ardent, unloved by their husband, and indifferent are false.
Conclusion: All she is false.
Peikoff says this is valid but I'm confused.
Middle Term: person who is ardent, unloved by her husband, and indifferent.
Minor Term: she
Major Term: false
Chart of Distributions
| Statement | Distribution of Subject | Distribution of Predicate |
|---|---|---|
| All she is a person who is ardent, unloved by her husband, and indifferent. | D | U |
| All persons who are ardent, unloved by their husband, and indifferent are false. | D | U |
| All she is false. | D | U |
Analysis
Does the syllogism have only 3 terms?
Yes.
Is the middle term distributed at least once?
Yes.
Are terms that are distributed the conclusion also distributed in the premises?
Yes.
Is no more than one of the premises negative?
Yes.
Is one of the premises negative? Then the conclusion must be negative.
NA.
Is the conclusion negative? Then one premise must be negative.
NA.
Argument is valid.
Problem 19 🤔
Sally didn’t get her hair done yesterday, because she got up late, and she gets her hair done only when she gets up on time.
My Attempt
Had a heck of a time breaking this down into premises and a conclusion. I decided to try breaking up Sallie into "Sallie" and "Late Sallie" and specifying that the background context of the statements is "yesterday:.
Identify the Components
Yesterday...
Premise: All Sally was Late Sallie.
Premise: No Late Sallie was getting hair done.
Conclusion: No Sally was getting hair done.
Middle Term: Late Sallie.
Minor Term: Sally.
Major Term: getting hair done.
Chart of Distributions
| Statement | Distribution of Subject | Distribution of Predicate |
|---|---|---|
| All Sally was Late Sallie. | D | U |
| No Late Sallie was getting hair done. | D | D |
| No Sally was getting hair done. | D | D |
Analysis
Does the syllogism have only 3 terms? Yes.
Is the middle term distributed at least once?
Yes.
Are terms that are distributed the conclusion also distributed in the premises?
Yes.
Is no more than one of the premises negative?
Yes.
Is one of the premises negative? Then the conclusion must be negative.
Yes.
Is the conclusion negative? Then one premise must be negative.
Yes.
Valid.
Peikoff's Approach
Peikoff's approach involves using the word "case" a lot.
Only cases of getting up in time are cases of hair done -> All cases of getting hair done are cases of getting up on time.
Identify the Components
Premise: All cases of getting hair done are cases of getting up on time.
Premise: No this case (of yesterday) is case of getting up on time.
Conclusion: No this case (of yesterday) is case of getting hair done.
Middle Term: cases of getting up on time.
Minor Term: this case (of yesterday)
Major Term: case of getting hair done.
Chart of Distributions
| Statement | Distribution of Subject | Distribution of Predicate |
|---|---|---|
| All cases of getting hair done are cases of getting up on time. | D | U |
| No this case (of yesterday) is case of getting up on time. | D | D |
| No this case (of yesterday) is case of getting hair done. | D | D |
Analysis
Does the syllogism have only 3 terms?
Yes.
Is the middle term distributed at least once?
Yes.
Are terms that are distributed the conclusion also distributed in the premises?
Yes.
Is no more than one of the premises negative?
Yes.
Is one of the premises negative? Then the conclusion must be negative.
Yes.
Is the conclusion negative? Then one premise must be negative.
Yes.
Problem 20 🤔 ❌
Down deep, all men really wish to be happy. The man who wishes to be happy, however, must make full, active use of his mind. Down deep, therefore, all men really make full, active use of their minds.
Identify the Components
Premise: All men are happiness-wanters.
Premise: All happiness-wanters are actively-minded.
Conclusion: Therefore, all men are actively-minded.
❌ ERRONEOUS: I think there is an ambiguity regarding "must" - an equivocation. The meaning could be "The man who wishes to be happy will, unavoidably due to his nature as a happiness-wanter, make full, active use of his mind" or "The man who wishes to be happy, in order to achieve that end, is required to volitionally choose to make full, active use of his mind." My second premise above reflects the "unavoidably" reading cuz that's the only way I saw to easily create a syllogism. I stopped at this point to listen to the lecture.
CORRECTION: Peikoff said it's Fallacy of Four Terms. That's basically an equivocation in the context of analyzing a syllogism. Peikoff says that for the second premise, the translation is something like: "All happy-wishers are men required to use their mind", hence four terms. After listening to Peikoff's discussion, I became convinced that the "must" had a pretty clear meaning and wasn't really ambiguous.
Problem 21 🤔
Identify the Components
It is ridiculous to claim that any course on logic improves the student’s thinking. I know, because I took a logic course once and my thinking was not only not improved, it positively deteriorated as a result.
I had trouble getting started on the analysis here. I wanted to say something like:
Premise: All I are a case of taking a logic class.
Premise: Some cases of taking logic classes are not thinking-improving.
Conclusion: No cases of taking logic classes are thinking-improving.
But that didn't seem right, so I just stopped and listened to the lecture.
Peikoff analyzes "It is ridiculous to claim that any course on logic improves the student’s thinking." as saying "all logic-course takers are improved" is false and therefore that, per the square of opposition, "some logic-course takers are not improved" is true. I originally read it differently, as saying that there were basically no effective logic courses. I think Peikoff's reading is better. His is like "It is ridiculous to claim that [taking] any course on logic improves the student’s thinking." and mine was more like "It is ridiculous to claim that any [existing] course on logic improves the student’s thinking."
So analyzing it Peikoff's way:
Premise: All I am logic course taker.
Premise: No I am improver.
Conclusion: Some logic-course takers are not improvers.
Middle Term: I
Minor Term: logic course taker
Major Term: improver
Chart of Distributions
| Statement | Distribution of Subject | Distribution of Predicate |
|---|---|---|
| All I am logic course taker. | D | U |
| No I am improver. | D | D |
| Some logic-course takers are not improvers. | U | D |
Analysis
Does the syllogism have only 3 terms?
Yes.
Is the middle term distributed at least once?
Yes.
Are terms that are distributed the conclusion also distributed in the premises?
Yes.
Is no more than one of the premises negative?
Yes.
Is one of the premises negative? Then the conclusion must be negative.
Yes.
Is the conclusion negative? Then one premise must be negative.
Yes.
Valid.