Math Problem

In this post, I'll be trying to understand the solution given to a math problem in Prealgebra from the Art of Problem Solving series by Richard Rusczyk.

Here is the problem:

What is the greatest number of acute interior angles that a decagon can have? (Note: the decagon may be concave!)

And here is the solution given for this problem:

I did not quite follow this solution, so I'm going to work up to understand it by working on simpler variants of the problem. This approach and various questions to ask in following it were suggested by a friend.

Triangles

Can a triangle have a reflex angle in it?

No. The internal angles have to sum to 180 degrees. A reflex angle exceeds 180 degrees (and is less than 360 degrees) by definition.

Another way to think about it is to suppose you have some point and you draw a single line segment extending out from it. Now suppose you want to draw another line segment out from the point. What's the biggest angle you can make at your point, between the two lines? 180 degrees, if you draw a straight line segment directly opposite your first line. If you do draw the line directly opposite the first line in this way - such that the angle between the two line segments is 180 degrees - then you can't actually make a triangle. To make a triangle, you need to connect the ends of the line segments you just drew together with a new line. But if they're directly opposite each other, then any line you draw between them is just gonna be overlapping the lines you've already drawn - you can't actually draw a new line and connect them. And really, if they're directly opposite each other, in a sense you don't even have two line segments ... even if you drew them separately, you basically have one line segment that you've divided in the middle. So you can't have a triangle with an angle even equal to 180 degrees, and a reflex angle is greater than 180 degrees, so it won't work.

Another way to think about it is to imagine you have a reflex angle and two line segments emanating from it. How many additional line segments do you need to "close" the shape? You need at least 2 more. You can't do it with one line.

Short Summary

Suppose an interior angle of a triangle, $r$, is a reflex angle that is greater than 180 degrees. We've already contradicted the definition of a triangle, since the interior angles of a triangle have to sum to 180 degrees and not exceed 180 degrees. The end.

What is the max number of obtuse angles a triangle can have?

1 obtuse angle maximum. If you try to have two obtuse angles, you won't be able to "close" the resulting shape in three lines. You may wind up with e.g. something that looks somewhat like an unfinished trapezoid, as in this illustration:

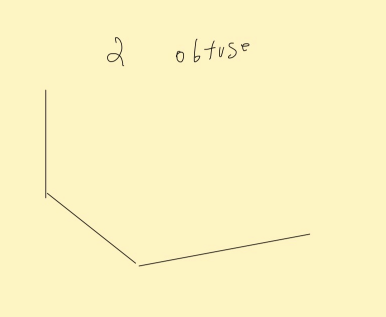
Formula & Testing

Suppose you have $n$ obtuse angles in your triangle. They can't be less than 90 degrees. So they take up GREATER THAN $90n$ of the 180 degrees of available interior angle of the triangle.

Any 2 given angles of a triangle cannot equal or exceed 180 degrees, or else forming an actual triangle becomes impossible.

If $n = 2$, $90n > 180$. This cannot be.

If $n = 1$, $90n > 90$, and a triangle can still be formed (e.g. one with angles 100-50-30).

$n=0$ is also acceptable (this would include e.g. an equilateral triangle).

Can a triangle have two right angles?

No. Here are two-right angles - note how it looks like an unfinished square:

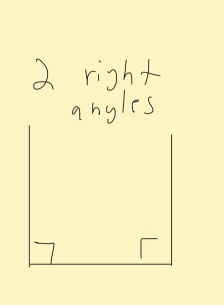
One way to put it: the angles of whatever shape you're drawing are gonna need to be greater than 180 degrees, and therefore not a triangle. We could "finish" the two right angle 📐 figure above and make it a square, but that would have interior angles = 4x = 360 degrees, so it is not a triangle...)

Formula & Testing

Suppose you have $n$ right angles in your triangle. They must be exactly 90 degrees. So they take up $90n$ of the 180 degrees of available interior angle of the triangle.

Any 2 given angles of a triangle cannot equal or exceed 180 degrees, or else forming an actual triangle becomes impossible.

If $n = 2$, $90n = 180$. This cannot be.

If $n = 1$, $90n = 90$, and a triangle can still be formed (specifically, a right angle).

$n=0$ is also acceptable (this would include e.g. an equilateral triangle).

Quadrilaterals

How many acute angles can a quadrilateral have?

A quadrilateral has 4 angles which have to total up to 360 degrees.

All 4 angles?

All 4 angles cannot be acute. If you try to draw a figure with 4 sides where each angle is acute, you wind up not being able to complete the figure:

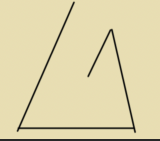
Another way to understand the issue: all 4 angles can't be acute because then the total of the 4 angles would not be equal to 360 degrees, but would instead be less than 360 degrees.

3 angles?

3 angles being acute seems mathematically possible in at least some cases. If you have 3 angles that are less than 90 degrees, and one angle that is greater than 90 degrees but less than 360 degrees, you can get a value equal to 360 degrees.

Obtuse

Can you have a quadrilateral where 3 interior angles are acute and one is obtuse? I didn't see any reason why not. I also found an interactive quadrilateral maker which I used to generate a quadrilateral consistent with this:

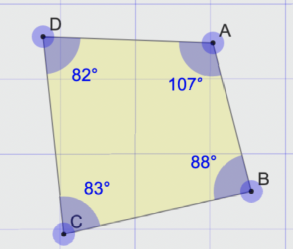
Reflex

What about a quadrilateral where there are 3 acute interior angles and one reflex angle (an angle greater than 180 degrees but less than 360)? E.g. 210 + 50 + 50 + 50? Again, I saw no reason why not, and guessed that it would probably be a convex shape. Here's another quadrilateral from the interactive maker (I'm going to try drawing my own first from now on but wanted to play with an interactive shape-manipulator some).

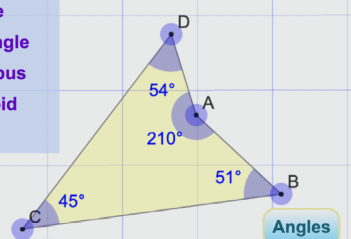
Formula & Testing

Suppose we have $n$ acute angles. Since we've defined them as acute, the sum of these angles must necessarily be less than $90n$ degrees according to our definition. Now we turn to consider the obtuse angles, of which we have $4 - n$. They must have interior angles which sum to less than $180(4 - n)$ (again, this is because of how we've defined them).

So the interior angles of the quadrilateral must be less than $90n + 180(4-n)$. This simplifies to $90n + 720 - 180n$ or $-90n - 720$.

Now let's consider what happens if we have 4 acute angles and we use that value in this expression that the interior angles of a quadrilateral must be less than. $-90(4) - 720 = 360$. Uhoh. We need our quadrilateral's interior angles to be less than this value, but by definition it's always going to equal this value.

Now let's consider what happens if we have 3 acute angles and we calculate that value. We get $-90(3) - 720 = 450$. That's good, cuz our quadrilateral's interior angles will always be less than 450 degrees.

Pentagons

How many acute angles can a pentagon have?

The interior angles of a pentagon need to sum up to $180(n - 2) = 540$ degrees. The acute angles need to be less than $90n$ and the obtuse angles need to be less than $360(5 - n)$ if we're permitting reflex angles/concave shapes. So the sum of the interior angles, 540, needs to be less than $90n + 360(5 - n)$, which simplifies to $-270n + 1800$. Or to put it similar to how the book puts in in the decagon problem, $-270n + 1800$ must be greater than 540 degrees.

If we have 5 acute angles, so $n = 5$, then we get $-270(5) + 1800 = 450$. A pentagon is always going to have interior angles that are greater than $450$, not less than $450$, so that won't work.

If we have 4 acute angles, we ultimately get a value of $820$. $540$ is indeed less than $820$, so that is an acceptable value. That means 4 acute angles will work.

Here's how we can use an inequality. We know that it's only possible to make a pentagon with $n$ acute angles if $-270n + 1800 > 540 degrees$. Another way of saying this is that we can only make a pentagon with $n$ acute angles if the value on the left is greater than the value on the right. If we perform algebraic manipulation on this inequality, we wind up with the following:

$2340 > 270n$

$4 \frac{2}{3} > n$

After algebraic manipulation, the statement "we can only make a pentagon with $n$ acute angles if the value on the left is greater than the value on the right is true. So we can only make a pentagon with $n$ acute angles if $4 \frac{2}{3}$ is greater than $n$. That means that $n$ can't be 5, but that it can be 4.

Decagons

Back to the original problem .

What is the greatest number of acute interior angles that a decagon can have? (Note: the decagon may be concave!)

The interior angles of a decagon must sum to $180(10 - 2)$ or 1440 degrees.

Suppose we have $n$ acute interior angles in the decagon. These have to be less than $90n$ degrees. The remaining interior angles have to be less than $360(10-n)$ degrees. Therefore, the interior angles of the decagon must sum to less than $90n + 360(10-n)$ degrees, or $-270n + 3600$ degrees (or, again, $-270n + 3600$ must be greater than 1440 degrees).

Consider the inequality $-270n + 3600 > 1440$. We can only have $n$ acute in our decagon angles if the expression on the left side exceeds the expression on the right side. Time to manipulate:

$-270n + 3600 > 1440$

$2160 > 270n$

$8 > n$

So 8 has to be greater than $n$ for us to have $n$ acute angles. So $n$ can't be 8, but it can be 7.