AOPS Pre-Algebra Selections - Chapter 10.3

Concepts - Polygons

The book defines polygon in the following way:

A polygon is a simple closed figure consisting entirely of line segments. By "closed figure," we mean that if we trace the entire figure, our start point and end point are the same. By "simple," we mean that the figure does not intersect itself. The line segments that form the boundaries of a polygon are the sides of the polygon. Three polygons are shown on the left below. Three figures that are not polygons are shown on the right below.

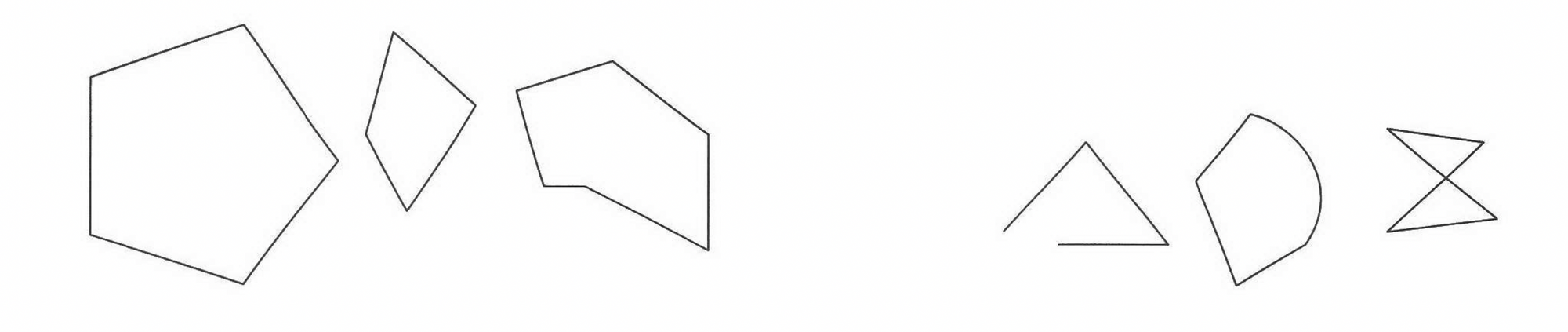
They don't really elaborate on the "line segment" aspect of the definition or explain the figures, but I think that the reason the middle figure on the right (which I also show below) is not a polygon is because it does not consist entirely of line segments on account of having a curve.

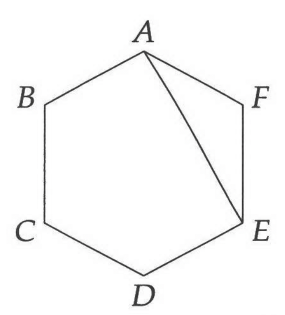
Line segments that form the boundaries of a polygon are the sides. Diagonals are formed when you connect two vertices that are not adjacent.

In-Chapter Problems

✅ Problem 10.20

a) 180°, since they're the interior angles of triangle.

b) 180°, since they're both on a line.

c) One way to thing of it is the sum of three line "angles" minus a triangle. So 540° - 180° = 360°.

d) In going around the triangle and turning as described, you wind up back in both your initial position and in the initial direction you were oriented in (facing B). The turning you do is represented by the sum of the exterior angles $x + y + z$. Since you wanted up facing the same place you started, the sum of these angles unsurprisingly wind up being 360°.

Exercises

❌ 10.3.4

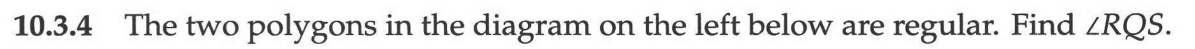
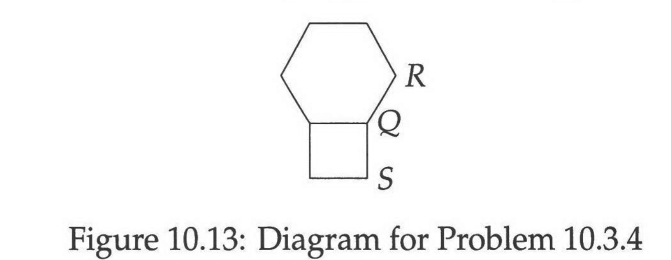
A regular hexagon has $\frac{180(6 - 2)}{6} = 120°$ interior angles and a square has 90° interior angles, so the sum of that, and thus the value of $\angle RQS$, is 210°.

(I'm assuming here that they are asking for the value of the angle that is interior to the conjoined polygons. If they wanted the exterior angle, it'd be 150°.)

NOTE: They wanted the exterior angle. I checked my notes and the last time I answered this, I came up with the answer they wanted. I think I generally look for angles within the interior of some shape unless it's specified that they want the exterior angle. I think the last time I did this, it must have struck me by the way the letters were arranged on the outside and by the fact that the interior angles were easy to determine that what they were asking for was the exterior angle (which involves an extra step from merely adding up the interior angles - namely, subtracting the sum of the interior angles from 360°). The question didn't strike me in the same way this time.

❌ 10.3.6

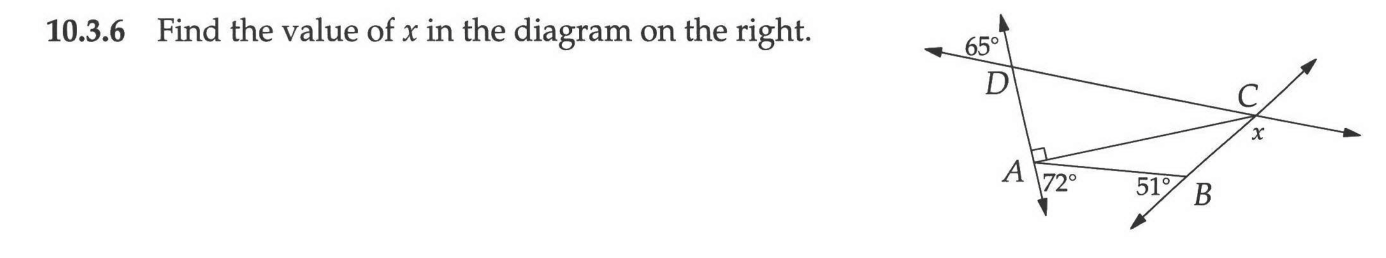
Since $\angle DAC$ is 90°, and an angle on the same line is 72°, then the other angle on the same line, $\angle BAC$, must be 18°.

$\angle ABC = 129°$ since it appears on the same line as a 51° angle.

NOTE: ERRORS START HERE

Therefore, $\angle ACB = 43°$.

$\angle DAC = 90°$ and $\angle ADC$ is vertical to a 65° angle and must therefore itself be 65°. Therefore $\angle DCA = 25°$.

The angle next to x is vertical to angles whose sum is 43° + 25° = 68°. Therefore, that angle must be 68°, and $x = 112°$.

NOTE: I made an arithmetic error. $\angle ABC = 129°$ and $\angle BAC = 18$, but the sum of those angles, 147°, means that angle $\angle ACB = 33°$, not 43° like I said. This means that the angle next to x = 58°, not 68°, and that $x = 122°$, not 112°.

✅ 10.3.9

If you follow along the outside of a polygon, then after traversing all the sides, you will wind up back in the same place you started. As the number of sides of a polygon increases, the sum of the interior angles increases, but the sum of the exterior angles, which represent the rotation or turning around the outside of a polygon, decreases correspondingly. The sum of the exterior angles decreases in such a manner that the sum of the exterior angles always winds up being 360°, even if the sum of the interior angles is very large.

For simplicity's sake, consider regular polygons. Consider a regular triangle. It has interior angles of 60°. Each exterior angle is thus 120°. And the sum of those 3 exterior angles is 360°. Now consider a regular pentagon. It has interior angles of 108°. Thus, its exterior angles are 72°, and the sum of those 5 exterior angles is ... 360°. The more sides a regular polygon has, the smaller the exterior angle for each interior angle.

They explained it a little differently:

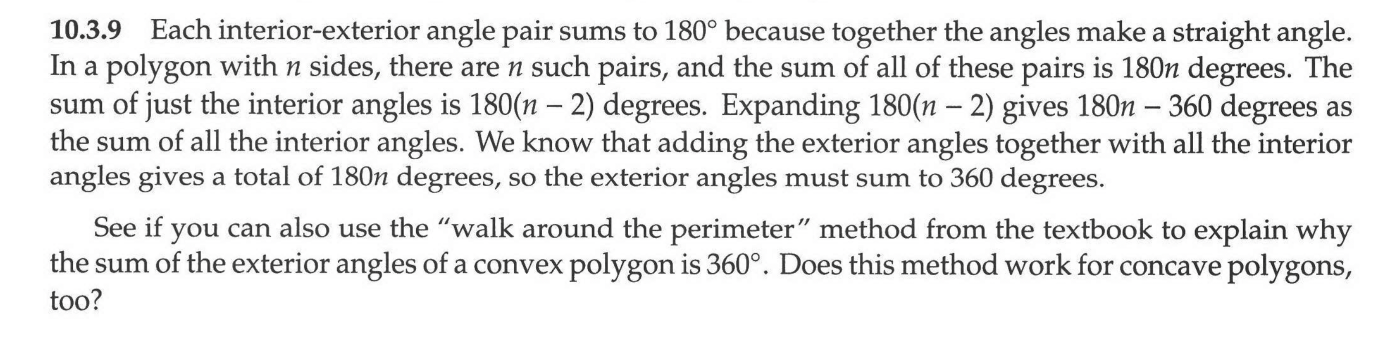
Regarding their question about concave polygons and the "walk around the perimeter method", my intuition is that the method may not work.

In a convex polygon like a triangle, if you extend the sides out past the vertices, you form the exterior angles and the sum of the interior and exterior angles, being on straight lines as they are, must sum to 180.

But in a concave polygon, even one of the interior angles of a polygon may exceed 180°, as does point C in the image I created below:

The exterior angles of a convex polygon represented the amount of turning/rotation you needed to do in the "walking around the perimeter" method. I think part of the assumptions of that method is that the exterior and interior angles are summing up to 180 degrees, so having an interior angle that exceeds 180° by itself seems to break things. I think there's more to figure out here.