AOPS Pre-Algebra Exercise 11.50 Deep Dive

This post will go into detail on Art of Problem Solving Pre-Algebra exercise 11.50.

The problem:

A hint from the book:

Initial Information

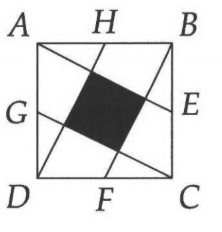
We know based on the information provided that the area of the square is 400 square units (we take $\overline{AB}$ and square that).

We also know that the length from a corner to a midpoint - e.g. $\overline{AH}$ - is 10.

We can figure out that the area of a triangle like $\triangle GDC$ is 100.

Solutions Using a Multi-Square Grid

One class of solutions involves using a multi-square grid like below (which Elliot Temple made) and using the patterns one can see as a result.

First we'll do some analysis of this grid, then we'll look at solutions.

Analysis: Counting Squares

Here is a list of squares and associated information (in formula form) that you can figure out from this image. Elliot Temple encouraged me to try this in this thread. Some information will be repeated/explained/elaborated below in the solutions section.

Let S = black square, T = small triangle, and P = trapezoid. There are 22 squares in the image.

1 square consisting of the entire picture, whose formula is $4S + 16P + 16T = 1600$

4 instances of the original square, whose formula is $S + 4P + 4T = 400$

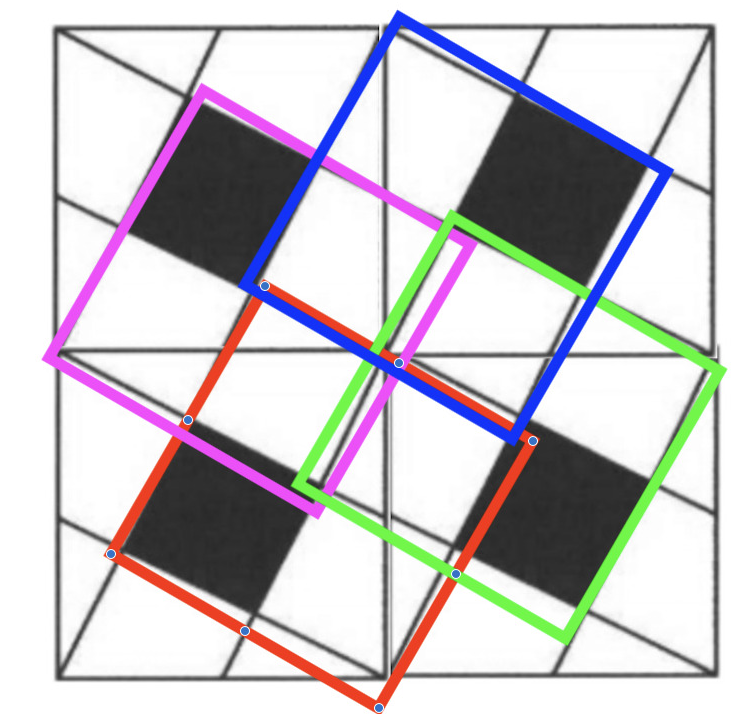
4 squares (above) whose formula is $S + 3T + 3P = 4T + 4P = 4S$

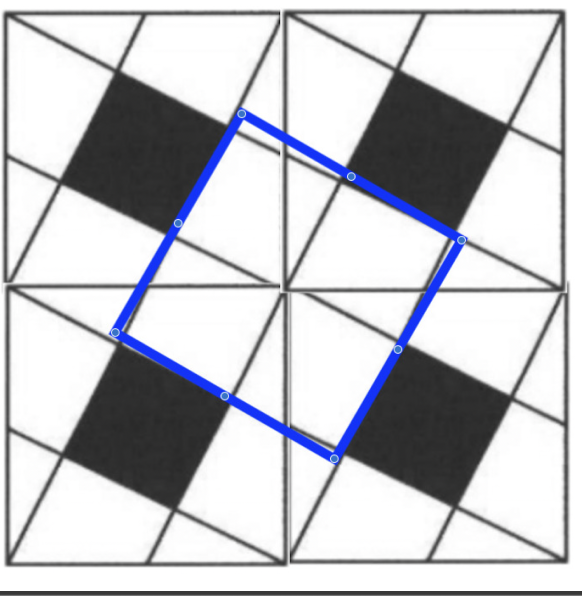
1 center square (above) whose formula is $4T + 4P = S + 3T + 3P = 4S$

4 black squares whose formula is $S = T + P$

8 smaller squares whose formula is $T + P = S$

Solutions

Comparing Two Large Squares Using Algebra

The original square had 1 black square, 4 small triangles, and 4 trapezoids. The area was 400. We can represent this as follows. Let S = black square, T = small triangle, and P = trapezoid:

$S + 4T + 4P = 400$

Using our grid of squares, we can identify a large square area that has a black square:

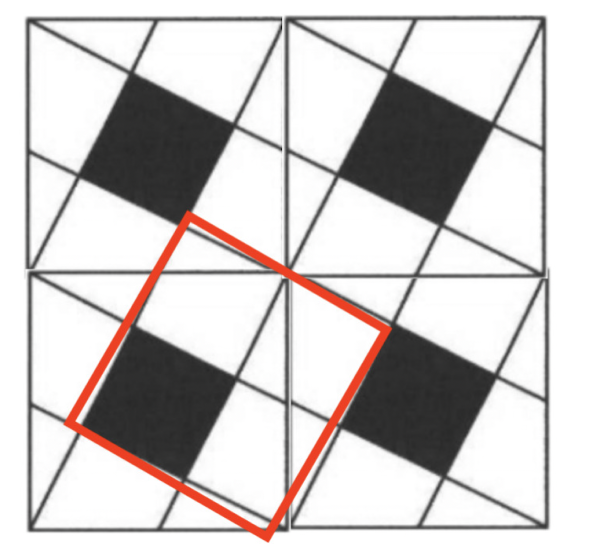
A formula for this square is $S + 3T + 3P$. We don't know the area.

Using our grid of squares, we can identify a square that appears to have the same area as the square we just identified but is composed of different elements:

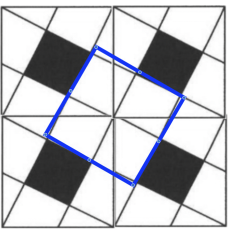
The formula for this square is $4T + 4P$.

Based on the shapes, we can set it equal to our previous square:

$4T + 4P = S + 3T + 3P$

We discover that $T + P = S$

This lets us substitute $T + P$ in our formula for the area of our original square.

$S + 4T + 4P = 400$

$S + 4(T + P) = 400$

$S + 4S + 400$

$5S = 400$

And so we can just solve for s

$S = 80$

So the area of the shaded area is 80.

Using Visual Similarity Between Components

If we look at the multi-square image and see that the black squares and the small triangle + trapezoid little squares are the same size, then we can just say that $T + P = S$ directly, without having to figure that out in terms of algebra on the bigger squares. Then we can use that information in the equation for our original square as before and solve the problem:

I. Equality of Black square and other small squares: $T + P = S$.

II. Original square: $S + 4P + 4T = 400$

Substitution of I into II: $S + 4S = 400$

$5S = 400$

$S = 80$

The multi-square image is very helpful to see this solution because there are no "whole" squares made out of a trapezoid and small triangle in the original image.

Book Solution

The book had a similar idea but used a different shape:

Solution Using Parallel Lines & Similar Triangles

Proving That There Are Parallel Lines

$\overline{HD}$ starts from a corner - point D - and in diagonally going across a square with sides of length 20, arrives at a point (H) on the other side that is 10 to the right of where it started.

$\overline{FB}$ starts at a midpoint - point F - and in diagonally going across the square, arrives at point B, which is 10 to the right of where it started.

So the lines, in "traveling" across a square of length 20, both "shifted over" to the right 10. So they maintained an identical distance from each other throughout. This indicates that they'll never meet, and are thus parallel.

Ingracke mentioned that "[a]nother way to think of it is that they have the same slope."

Proving Similar Triangles

$\overline{HD}$ and $\overline{FB}$ are parallel lines (see above). They're going to make the same angles when they intersect $\overline{GC}$, so $\angle DLC$ and $\angle FKC$ are the same. Since $\triangle DLC$ and $\triangle FKC$ share $\angle C$, all the angles in the triangles must be the same, and so the triangles are similar.

$\triangle LDC$ is the larger of the two triangles. We know from a straightforward application of the information we are given that line FC (the hypotenuse of triangle KFC) is 10 long and line DC (the hypotenuse of triangle LDC) is 20 long. So triangle LDC is a 2X scaled up version of triangle KFC.

Finishing the Solution

If the bigger of two similar triangles is a 2 times scaled up version of the smaller triangle, then its base and height will be twice as long as the smaller similar triangle. This means the area will be 4 times that of the smaller similar triangle.

The hypotenuse of the bigger similar triangle $\triangle LDC$ is 2x that of the smaller triangle $\triangle KFC$.

The area of $\triangle GDC = 100$. $\triangle GDC$ consists of one of the bigger similar triangles - $\triangle LDC$ - and one of the smaller ones - $\triangle DLG$. Another way of saying this is that it consists of the area of 5 of the smaller similar triangles - one area of a smaller triangle and one area of a larger triangle that is equal to 4 smaller triangles.

Let $s$ stand for the area of the smaller similar triangles.

$5s = 100$

$s = 20$

We know that the bigger of the similar triangles, $\triangle LDC$, is equal to $4s$. We now know that the area represented by that triangle is 80. There are four interlocking such triangles, so their total area is 320. The total area of the square is 400, so the difference between the 4 interlocking big triangles and the total area gives us the shaded area. That is $400 - 320 = 80$.

Solution by Rotating Elements

Imagine rotating the elements of the original square around so that you get a "cross" of 5 squares.

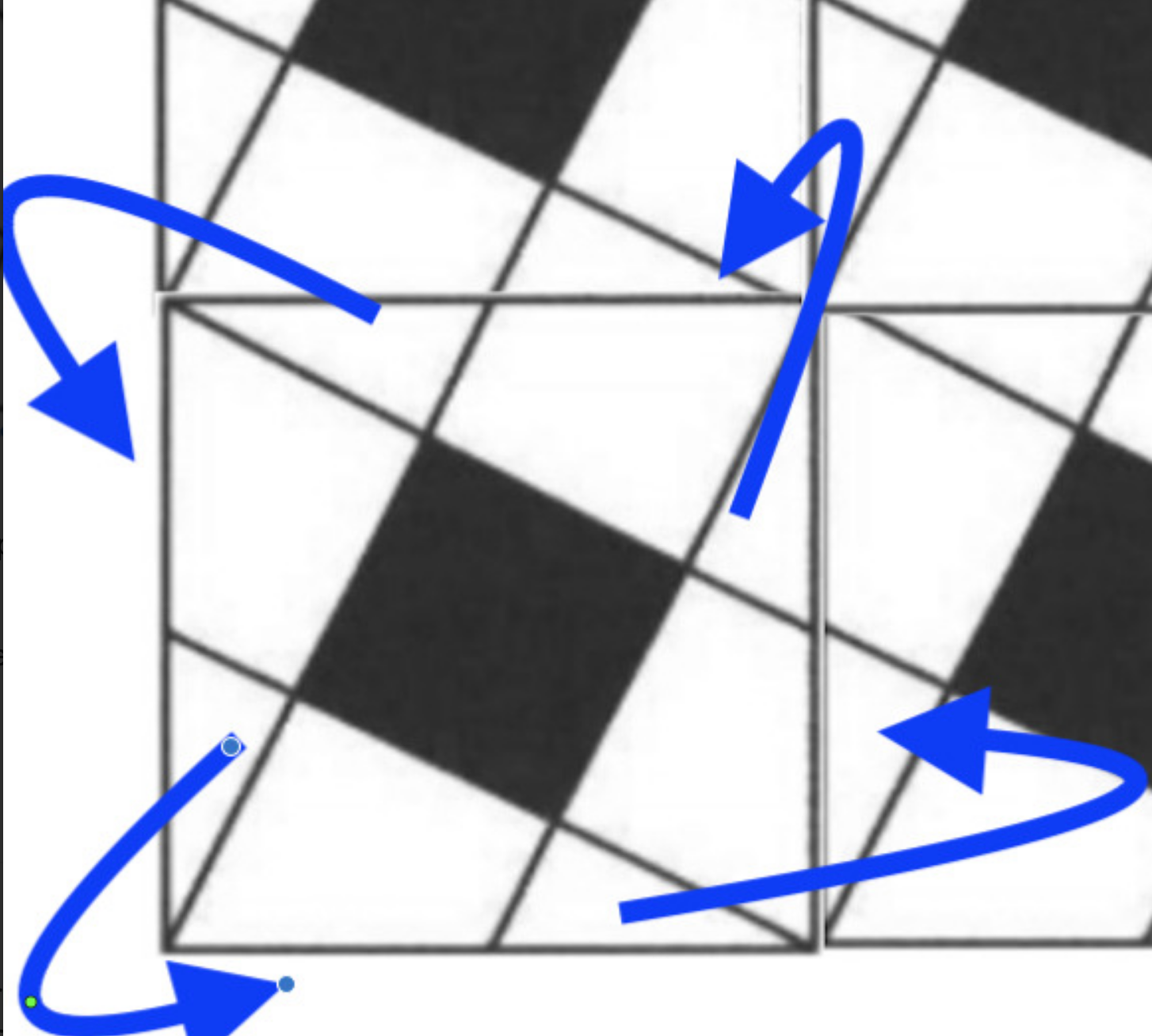
For example, you move the small triangle with side FC around so that it would “complete” the trapezoid with side EC.

So with that approach you’d have 5 squares of the same size, which you knew had a total area of 400, and you could just divide the area by the 5 squares to get the area of one square (such as the shaded).