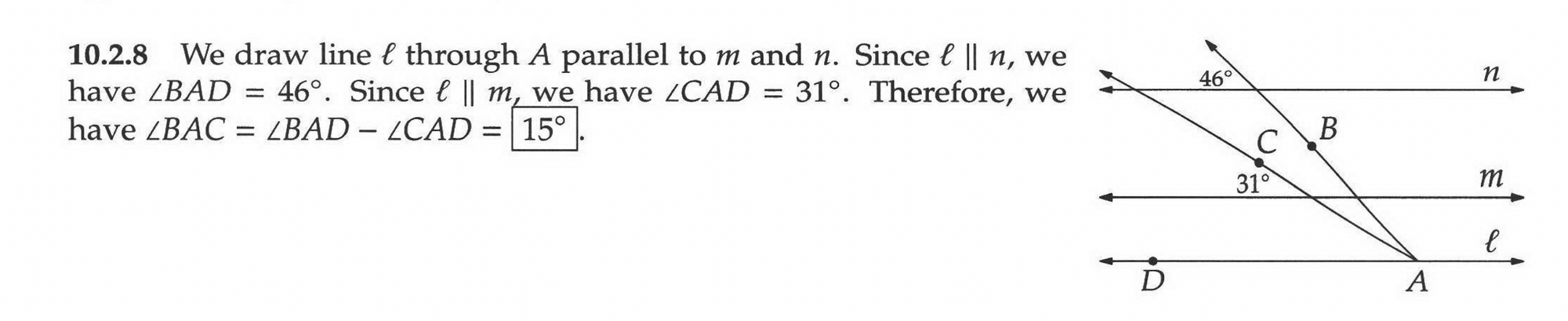AOPS Pre-Algebra Chapter 10.2 Selections - Parallel Lines
Table of Contents
Concept - Transversals
Transversals - line that cuts across parallel lines and creates angles with the same measure.
One way to see why is to imagine sliding line $\overleftrightarrow{D F}$ on top of $\overleftrightarrow{C G}$ so that point $B$ is on top of point $A$. Then, $\angle ABF$ would be right on top of $\angle HAG$. This isn't a proof, but it does give us some idea why these angles have the same measure.

Important point: if you determine that angles on different lines have the same measure, you can reason from that to the fact that the lines are parallel.

In-Chapter Problems
✅ Problem 10.11

If we run a line through point Y and divide the 71° angle, then we can figure things out (see image below).
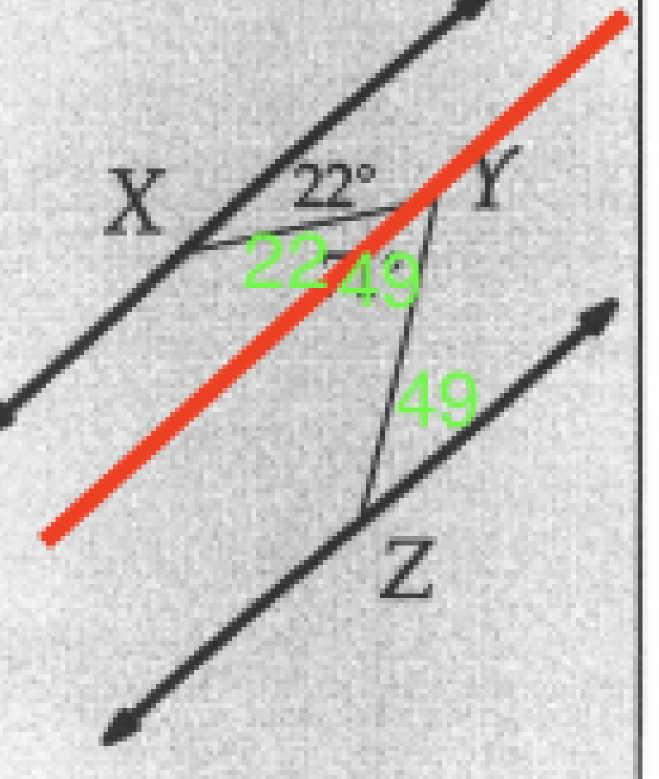
The line running from point X to point Y creates acute angles of 22° at both lines. This means the acute angle at point Y other than the 22° angle is 49° - the angle there used to be 71°, but we split it, and we know the other angle is 22°, and 71° - 22° = 49°.
The line that runs from Y to Z thus creates acute angles of 49°. So the answer to the question is 49°.
Exercises
✅ 10.2.1
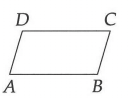
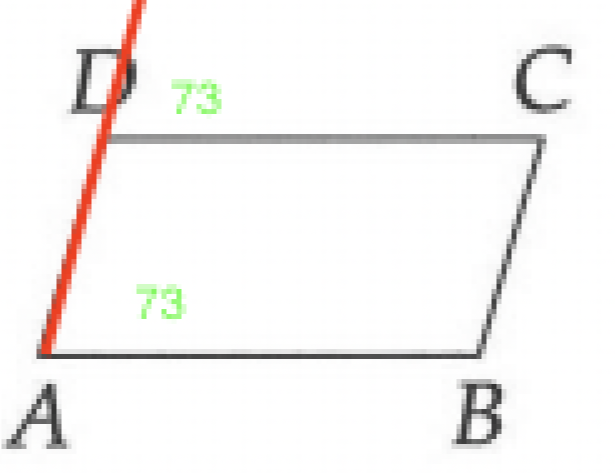
Imagine $\overline{AD}$ extended past $\overline{DC}$. The acute angle on that extended line lying "outside" the current parallelogram would have to be 73° by the logic of the transversal stuff we learned. By the rule that the angles on a straight line have to add up to 180°, then, $\angle ADC$ would have to be 107°. And then again by the rule about summing to 180°, $\angle C$ would have to be 73°.
✅ 10.2.5

Nine. If the lines are parallel, then the total number of regions is always $n + 1$ the number of lines where n is the number of lines. So with 1 line you get 2 regions, with 2 you get 3, and so on.
They explained it a bit differently:
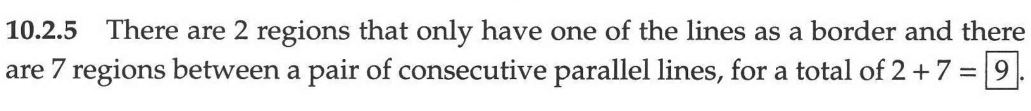
✅ 10.2.6

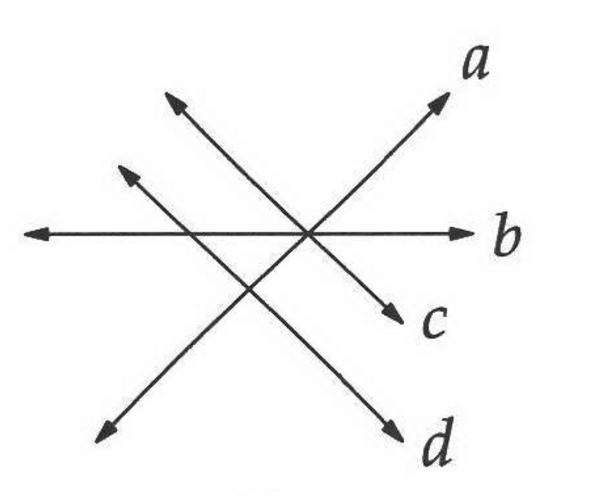
If d is perpendicular to a and parallel to c, then c is also perpendicular to a. Therefore, the angle next to the acute angle between a and b must be 90°.
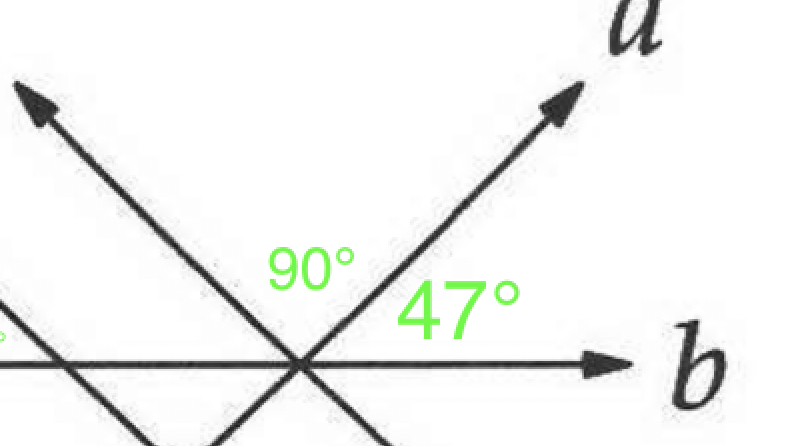
That means that that the angle clockwise from that 90 degree angle must be 43°, since the angles on line b must sum to 180.
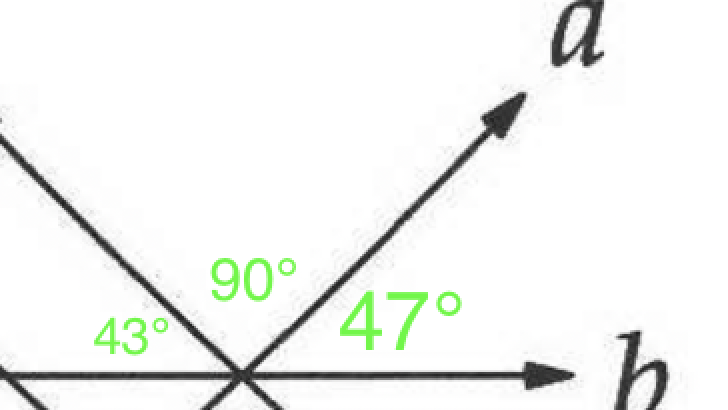
Since c and d are parallel and b is a transversal cutting across them, the acute angle between b and d must also be 43°.
✅ 10.2.8

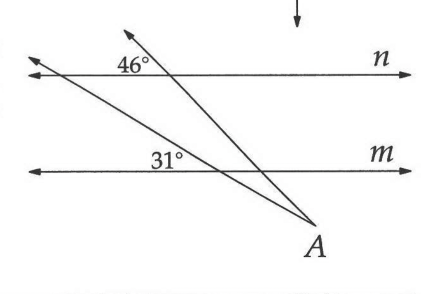
If we add another line down by point A, we can draw a curve from ray a (my label) that represents the same 46° angle as on line n. But we see that ray b (my label) is using up some of the space of that angle, and by the rules of transversals, we can see that it's using up 31° of that angle. So the angle we're actually looking for is 46° - 31° or 15°.
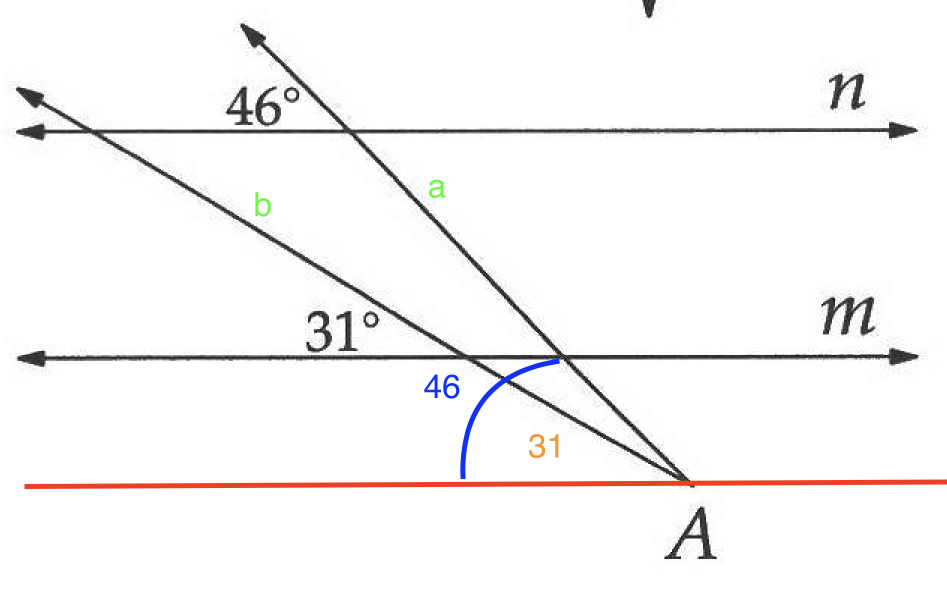
They explained it a bit differently: